![[论文理解] DENOISING DIFFUSION IMPLICIT MODELS](https://sunlin-ai.github.io/images/albumsbg.jpg)
DDPM 样本生成过程缓慢， DDIM 的提出是为了解决 DDPM 样本生成缓慢问题。
动机
DDPM 的采样是根据上一步采样结果 \(\mathbf{x}_t\) 逐步生成下一步结果 \(\mathbf{x}_{t-1}\)，所以不能跨越步骤，如果扩散过程的时间步为1000，则生成过程的时间步也需要设置为1000，带来的问题是样本生成过程缓慢。
DDIM 的提出是为了解决 DDPM 样本生成缓慢问题，思路是根据 \(\mathbf{x}_t\) 先预测 \(\mathbf{x}_0\)，然后根据 \(\mathbf{x}_0\) 再预测 \(\mathbf{x}_{t-1}\) ，这里可以将 \(\mathbf{x}_0\) 看作一个跳板，生成过程可以设置任意的时间步，摆脱了 DDPM 时间步的限制。
DDIM 的扩散过程、训练和 DDPM 类似，关于DDPM的详细理解参见前面博客1，主要不同点在于采样过程，两者对比如下图，DDIM 的样本生成过程不再是马尔科夫链，因为 \(\mathbf{x}_{t-1}\) 不仅依赖 \(\mathbf{x}_t\) ,也依赖 \(\mathbf{x}_0\)。
扩散过程
DDIM 扩散过程和 DDPM一致，即：
\[q(\mathbf{x_t} \vert \mathbf{x_{t-1}}) = \mathcal{N}(\mathbf{x_t}; \sqrt{1 - \beta_t} \mathbf{x_{t-1}}, \beta_t\mathbf{I}),\]由上式进一步推导，当已知初始状态\(\mathbf{x_0}\)，可以采样得到任意step \(t\) 的 \(\mathbf{x_{t}}\)，上式又可以表示成：
\[q(\mathbf{x_t} \mid \mathbf{x_0}) = \mathcal{N}(\mathbf{x_t}; \sqrt{\alpha_t} \mathbf{x_0}, (1 - \alpha_t)\mathbf{I}).\]实现代码2：
def q_xt_x0(x0, t):
mean = gather(alpha_bar, t) ** 0.5 * x0 # now alpha_bar
var = 1-gather(alpha_bar, t) # (1-alpha_bar)
eps = torch.randn_like(x0)
return mean + (var ** 0.5) * eps
生成过程
DDPM 根据 Bayes rule：
\[\begin{aligned} q\left(\mathbf{x_{t-1}} \mid \mathbf{x_{t}}, \mathbf{x_{0}}\right)=& \frac{q\left(\mathbf{x_{t}} \mid \mathbf{x_{t-1}}\right) q\left(\mathbf{x_{t-1}} \mid \mathbf{x_{0}}\right)}{q\left(\mathbf{x_{t}} \mid \mathbf{x_{0}}\right)} \\ =&\mathcal{N}\left(\mathbf{x_{t-1}} ;\frac{1}{\sqrt{\alpha_{t}}}\left(\mathbf{x_{t}}-\frac{\beta_{t}}{\sqrt{1-\alpha_{t}}} \mathbf{\epsilon}\right),\frac{1-\alpha_{t-1}}{1-\alpha_{t}} \beta_{t} \mathbf{I}\right) \end{aligned}\]DDIM 3使用另一个方法推导 \(q\left(\mathbf{x_{t-1}} \mid \mathbf{x_{t}}, \mathbf{x_{0}}\right)\)
因为：
\[q_\sigma(\mathbf{x}_t \vert \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_t; \sqrt{\alpha_t} \mathbf{x}_0, (1 - \alpha_t)\mathbf{I}),\]可以推导出：
\[q_{\sigma}(\mathbf{x_{t-1}} \mid \mathbf{x_0}) = \mathcal{N}(\mathbf{x_{t-1}}; \sqrt{\alpha_{t-1}} \mathbf{x_0}, (1 - \alpha_{t-1})\mathbf{I}),\]则：
\[\begin{aligned} \mathbf{x_{t-1}} &= \sqrt{\alpha_{t-1}}\mathbf{x_0} + \sqrt{1 - \alpha_{t-1}}\cdot\mathbf{\epsilon_{t-1}} \\ &= \sqrt{\alpha_{t-1}}\mathbf{x_0} + \sqrt{1 - \alpha_{t-1} - \sigma_t^2} \cdot\mathbf{\epsilon_t} + \sigma_t\mathbf{\epsilon} \\ \end{aligned},\]为什么 \(\sqrt{1 - \alpha_{t-1}}\cdot\mathbf{\epsilon}_{t-1}\) 可以写成 \(\sqrt{1 - {\alpha_{t-1}} - \sigma_t^2} \cdot\mathbf{\epsilon_t} + \sigma_t\mathbf{\epsilon}\) ？
根据高斯分布的性质，两个高斯分布 \(x\sim \mathcal{N}(0, a)\) 和 \(y\sim \mathcal{N}(0, b)\) , 则 \(x+y \sim \mathcal{N}(0, \sqrt{a^2+b^2})\) , 因为 \(\mathbf{\epsilon_{t-1}}\) 和 \(\mathbf{\epsilon}\) 都是高斯分布，所以：
\[\sqrt{1 - \alpha_{t-1} - \sigma_t^2} \cdot\mathbf{\epsilon}_t + \sigma_t\mathbf{\epsilon}=\sqrt{1 - \alpha_{t-1} - \sigma_t^2+ \sigma_t^2} \cdot\mathbf{\epsilon}_{t-1}=\sqrt{1 - \alpha_{t-1}}\cdot\mathbf{\epsilon}_{t-1},\]因为 \(\mathbf{x_t} = \sqrt{\alpha_t}\mathbf{x_0} + \sqrt{1 - \alpha_t}\mathbf{\epsilon}\) ，所以 \(\mathbf{x}_0\) 可以根据 \(\mathbf{x}_t\) 计算出来：
\[\mathbf{x_0}= \frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x_t}-\sqrt{1 - \alpha_t}\cdot\mathbf{\epsilon_{\theta}}^{(t)}(\mathbf{x_t})\right),\]代入 \(\mathbf{x}_0\) ，得到最终 DDIM 的样本生成过程如下：
\[\boldsymbol{x}_{t-1}=\sqrt{\alpha_{t-1}} \underbrace{\left(\frac{\boldsymbol{x}_{t}-\sqrt{1-\alpha_{t}} \epsilon_{\theta}^{(t)}\left(\boldsymbol{x}_{t}\right)}{\sqrt{\alpha_{t}}}\right)}_{\text {"predicted } \boldsymbol{x}_{0} \text { " }}+\underbrace{\sqrt{1-\alpha_{t-1}-\sigma_{t}^{2}} \cdot \epsilon_{\theta}^{(t)}\left(\boldsymbol{x}_{t}\right)}_{\text {“direction pointing to } \boldsymbol{x}_{t} \text { " }}+\underbrace{\sigma_{t} \epsilon_{t}}_{\text {random noise }},\]式中： \(\epsilon_{t} \sim \mathcal{N}(\mathbf{0}, \boldsymbol{I})\)，并且定义 \(\sigma_{t}:=\eta\sqrt{\left(1-\alpha_{t-1}\right) /\left(1-\alpha_{t}\right)} \sqrt{1-\alpha_{t} / \alpha_{t-1}}\) ， \(\alpha_{0}:=1\).
实现代码：
def p_xt(xt, noise, t,next_t):
at = compute_alpha(beta, t.long())
at_next = compute_alpha(beta, next_t.long())
x0_t = (xt - noise * (1 - at).sqrt()) / at.sqrt()
c1 = (eta * ((1 - at / at_next) * (1 - at_next) / (1 - at)).sqrt())
c2 = ((1 - at_next) - c1 ** 2).sqrt()
eps = torch.randn(xt.shape, device=xt.device)
xt_next = at_next.sqrt() * x0_t + c2 * noise+ c1 * eps
return xt_next
当 \(\eta=1\)时，前向过程就变成了 Markovian, 生成过程也成了 DDPM；
当 \(\eta=0\) 时，给定 \(\boldsymbol{x_0}\) 和 时 \(\boldsymbol{x_{t-1}}\) ，此时除了 \(t=1\)，其余时刻的前向过程变成确定性的，对隐变量使用固定的过程生成样本，这被称为 “ 去噪扩散隐式模型 (denoising diffusion implicit model ,DDIM) ”。
下表显示了不同 \(\eta\) 取值的效果，可见 \(\eta\) 取值越低，生成效果越好。
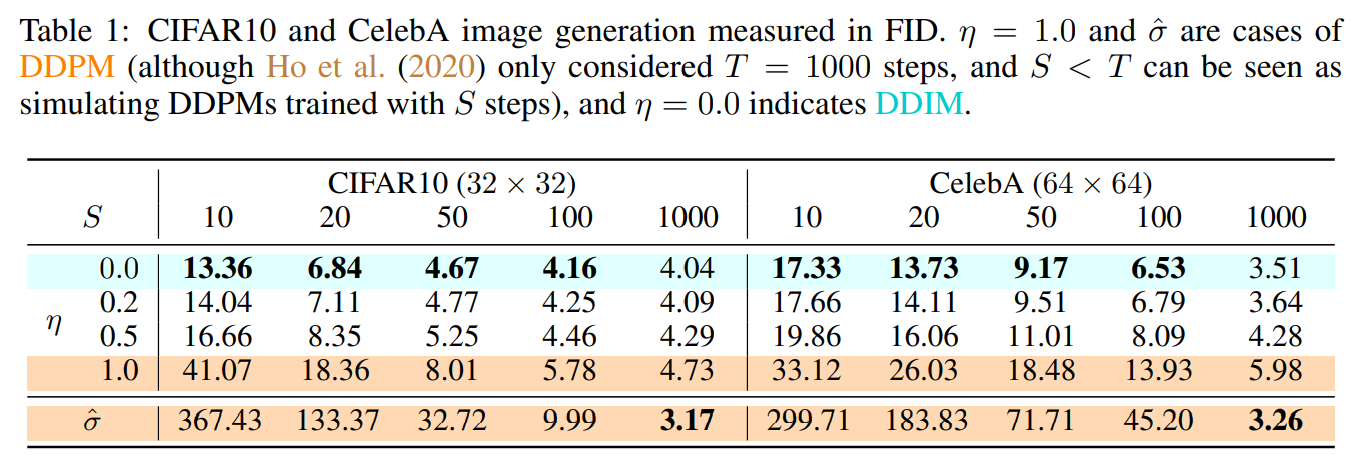
\(\tau\) 表示生成样本的时间步数 ，假设扩散过程的时间步数为20， 设置生成过程时间步数为 10，则扩散过程和生成过程的时间步如下，可以大大提高样本生成速度。
扩散过程时间步：[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19]
生成过程时间步：[0, 2, 4, 6, 8, 10, 12, 14, 16, 18]
下图为不同 \(\tau\) 和 \(\eta\) 组合的效果，总体而言 \(\tau\) 越大，图片质量越清晰，但是会牺牲样本生成速度。
输入一张带噪声的图片，通过 unet 模型预测噪声，然后反向生成样本，图像逐步恢复成无噪声的状态。
eta=0.0
n_steps=1000
timesteps=50
n = x.size(0)
skip = n_steps // timesteps
seq = range(50, n_steps, skip)
seq_next = [-1] + list(seq[:-1])
for i, j in zip(reversed(seq), reversed(seq_next)):
t = (torch.ones(n) * i).cuda()
next_t = (torch.ones(n) * j).cuda()
with torch.no_grad():
pred_noise = unet(x, t)
x = p_xt(x, pred_noise, t, next_t)
参考
-
sunlin,DDIM colab code ↩
-
Jiaming Song, Chenlin Meng, Stefano Ermon, “Denoising Diffusion Implicit Models”, International Conference on Learning Representations, 2021. ↩