Google Brain 推出的 Imagen1,再一次突破人类想象力,将文本生成图像的逼真度和语言理解提高到了前所未有的新高度!比前段时间 OpeAI 的 DALL·E 2 2更强!
Imagen
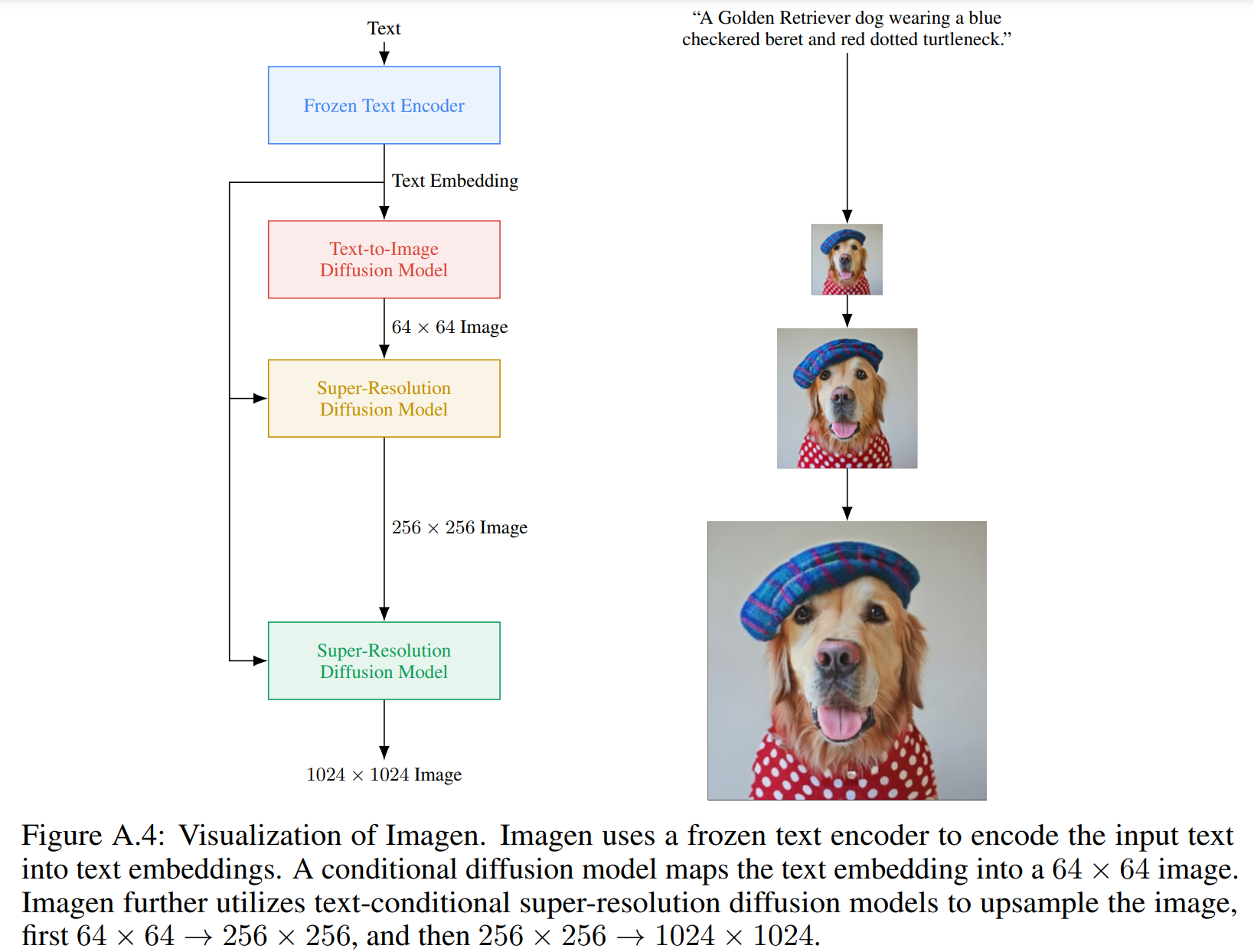
Imagen 的组成:(1) 文本编码器,用于将文本映射成 embeddings 序列 ;(2) 级联条件扩散模型,用于将 embeddings 序列映射成图像,并逐步增加图像分辨率(参见 图 A.4),以下将详细描述这些组件。
文本编码器
文本图像模型需要强大的语义文本编码器来捕获任意自然语言文本输入的复杂性和组合性。
在当前的文本到图像模型中通常使用在配对的图文数据集上训练的文本编码器,比如 CLIP。大型的语言模型可以作为另一种选择,例如 BERT、 GPT、 T5 , 语言模型在纯文本语料库上训练,训练数据远多于成对的图像-文本数据, 所以其可以接触更加丰富和广泛分布的文本。语言模型通常也大得多(例如,PaLM 有 540 B 参数,而 CoCa 有1B 参数)。
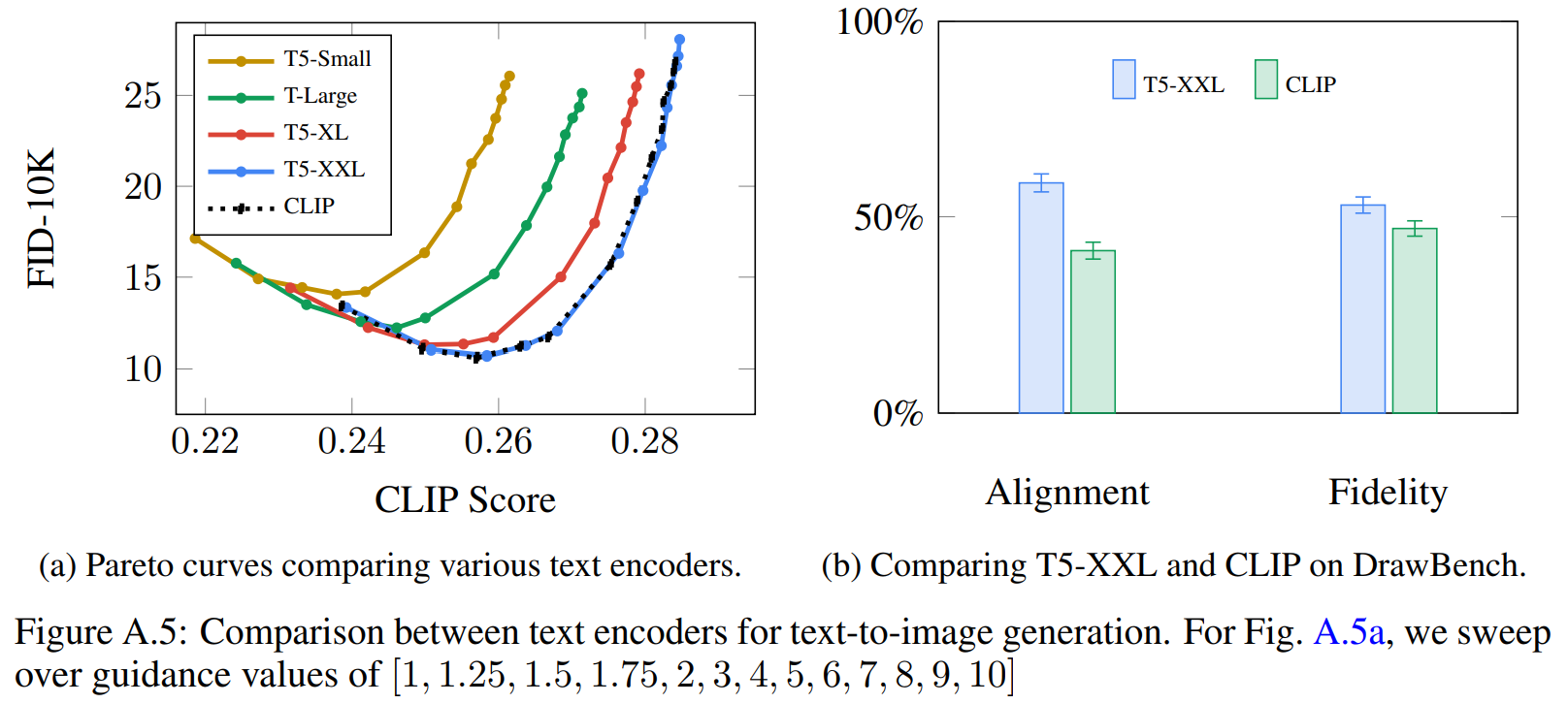
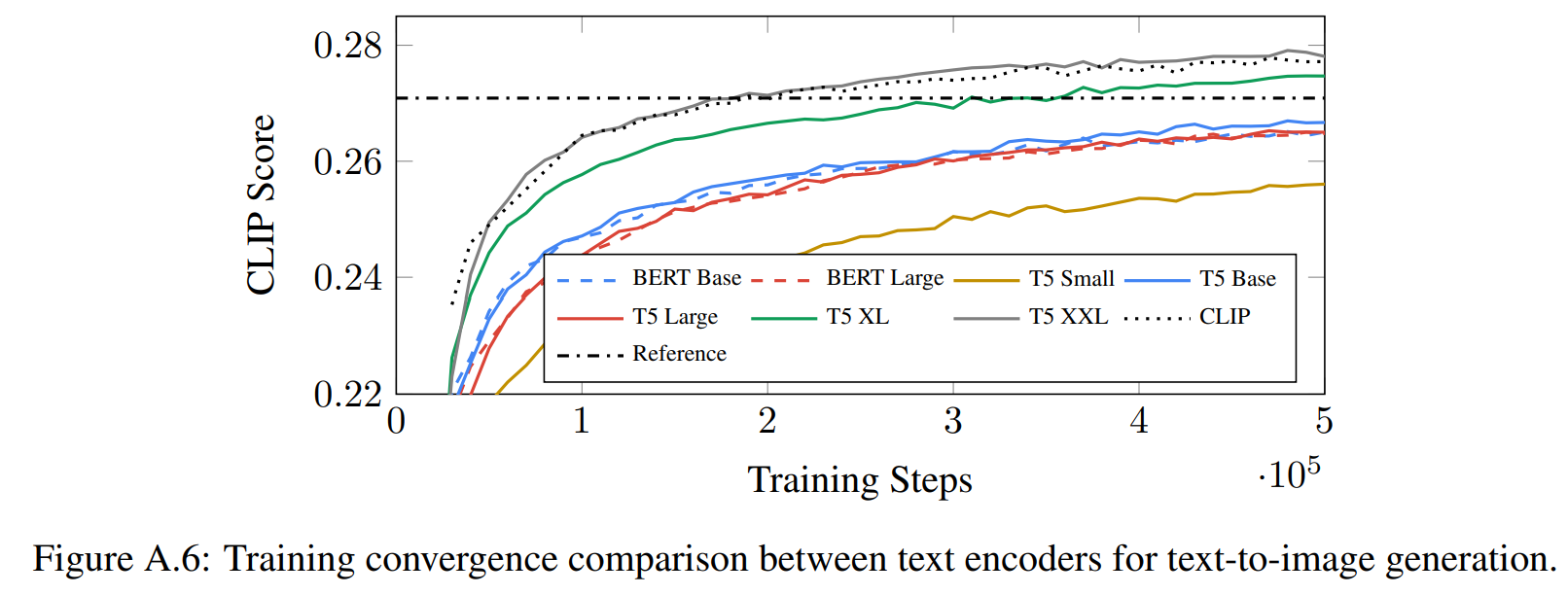
Imagen 研究比较了预训练文本编码器:BERT 、T5 和 CLIP。这些文本编码器的权重是冻结的,这样做的好处是可以离线计算文本嵌入,在训练文本到图像生成模型期间,计算或内存占用可以忽略不计。经过实验比较发现文本编码器大小会影响文本到图像生成质量, T5-XXL 在图像-文本对齐、图像逼真度方面可以取得最好的成绩。
无分类器指导的扩散模型
(1)扩散过程
\(\mathbf{z}_{t}=\alpha_{t} \mathbf{x}+\sigma_{t} \boldsymbol{\epsilon_1}\),其中 \(\boldsymbol{\epsilon} \sim \mathcal{N}(\mathbf{0}, \mathbf{I})\)。
根据正向过程的定义可得:\(\mathbf{z}_s=\alpha_s \mathbf{x}+\sigma_s \boldsymbol{\epsilon_2}\) ,则 \(\mathbf{x}=\frac{1}{\alpha_s}(\mathbf{z}_s-\sigma_s \boldsymbol{\epsilon_2})\),将 \(\mathbf{x}\) 代入上式得:
\[\mathbf{z}_{t}=\frac{\alpha_{t}}{\alpha_s}(\mathbf{z}_s-\sigma_s \boldsymbol{\epsilon}_2)+\sigma_{t} \boldsymbol{\epsilon_1}=\frac{\alpha_{t}}{\alpha_s}\mathbf{z}_s-\frac{\alpha_{t}\cdot\sigma_s}{\alpha_s}\boldsymbol{\epsilon}_2+\sigma_{t} \boldsymbol{\epsilon_1}=\frac{\alpha_{t}}{\alpha_s}\mathbf{z}_s+\sqrt{\sigma_{t}^2-\frac{\alpha_t^2\cdot\sigma_s^2}{\alpha_s^2}}\cdot\epsilon\](上式中,两个正太分布相减,其方差应该是相加,但是根据论文的推导方差为相减,这里是个疑问 )
定义:\(\sigma_{t \mid s}^{2}=\left(1-e^{\lambda_{t}-\lambda_{s}}\right) \sigma_{t}^{2}\) ,其中 \(\lambda_{t}=\log \left[\alpha_{t}^{2} / \sigma_{t}^{2}\right]\),则:
\[\mathbf{z}_{t}=\left(\alpha_{t} / \alpha_{s}\right) \mathbf{z}_{s}+\sqrt{\sigma_{t \mid s}^{2}}\cdot\epsilon\]所以:
\[q\left(\mathbf{z}_{t} \mid \mathbf{x}\right)=\mathcal{N}\left(\mathbf{z}_{t} ; \alpha_{t} \mathbf{x}, \sigma_{t}^{2} \mathbf{I}\right), \quad q\left(\mathbf{z}_{t} \mid \mathbf{z}_{s}\right)=\mathcal{N}\left(\mathbf{z}_{t} ;\left(\alpha_{t} / \alpha_{s}\right) \mathbf{z}_{s}, \sigma_{t \mid s}^{2} \mathbf{I}\right)\]式中, \(0 \leq s<t \leq 1, \sigma_{t \mid s}^{2}=\left(1-e^{\lambda_{t}-\lambda_{s}}\right) \sigma_{t}^{2}\), \(\alpha_{t}, \sigma_{t}\) 表示可微噪声schedule, \(\lambda_{t}=\log \left[\alpha_{t}^{2} / \sigma_{t}^{2}\right]\) 表示信噪比,其随着时间 \(t\) 逐步降低,直到 \(q\left(\mathbf{z}_{1}\right) \approx \mathcal{N}(\mathbf{0}, \mathbf{I})\)。
(2)生成过程
反转上述扩散过程,可以看作学习解噪 \(\mathbf{z}_{t} \sim q\left(\mathbf{z}_{t} \mid \mathbf{x}\right)\) ,即根据 \(\mathbf{z}_{t}\) 和其他条件估计 \(\mathbf{x}\) ,可以表示成:
\[\hat{\mathbf{x}}_{\theta}\left(\mathbf{z}_{t}, \lambda_{t}, \mathbf{c}\right) \approx \mathbf{x}\]式中, \(\mathbf{c}\) 为可选的条件信息(比如文本embeddings 或者低分辨率图像)。训练 \(\hat{\mathbf{x}}_{\theta}\) 使用加权 MSE 损失函数:
\[\mathbb{E}_{\boldsymbol{\epsilon}, t}\left[w\left(\lambda_{t}\right)\left\|\hat{\mathbf{x}}_{\theta}\left(\mathbf{z}_{t}, \lambda_{t}, \mathbf{c}\right)-\mathbf{x}\right\|_{2}^{2}\right]\]式中, \((\mathbf{x}, \mathbf{c})\) 是 数据-条件对, \(t \sim \mathcal{U}([0,1]), \boldsymbol{\epsilon} \sim \mathcal{N}(\mathbf{0}, \mathbf{I})\), \(\alpha_{t}, \sigma_{t}, w_{t}\) 是关于 \(t\) 的函数,其影响样本生成质量。
因为 \(\mathbf{z}_{t}=\alpha_{t} \mathbf{x}+\sigma_{t} \boldsymbol{\epsilon}\),对 \(\epsilon\) 参数化,则 \(\hat{\mathbf{x}}_{\theta}\left(\mathbf{z}_{t}, \lambda_{t}, \mathbf{c}\right)=\left(\mathbf{z}_{t}-\sigma_{t} \epsilon_{\theta}\left(\mathbf{z}_{t}, \lambda_{t}, \mathbf{c}\right)\right) / \alpha_{t}\) ,所以损失函数可以简化为:
\[\mathbb{E}_{\boldsymbol{\epsilon}, t}\left[w\left(\lambda_{t}\right)\left\|\epsilon_{\theta}\left(\mathbf{z}_{t}, \lambda_{t}, \mathbf{c}\right)-\epsilon\right\|_{2}^{2}\right]\]训练模型时,使用 Classifier-free guidance 方法,在单个扩散模型上同时训练无条件和带条件目标,具体做法是在训练模型时随机(一般以 \(10 \%\) 的概率)丢弃 \(\mathbf{c}\),得到 \(\epsilon_{\theta}(\mathbf{z}_{t},\lambda_{t},\mathbf{c})\) 之后,使用下式更新:
\[\tilde{\boldsymbol{\epsilon}}_{\theta}\left(\mathbf{z}_{t}, \lambda_{t}, \mathbf{c}\right)=w \boldsymbol{\epsilon}_{\theta}\left(\mathbf{z}_{t}, \lambda_{t}, \mathbf{c}\right)+(1-w) \boldsymbol{\epsilon}_{\theta}\left(\mathbf{z}_{t}, \lambda_{t}\right)\]式中, \(\boldsymbol{\epsilon}_{\theta}\left(\mathbf{z}_{t}, \lambda_{t}, \mathbf{c}\right)\) 和 \(\boldsymbol{\epsilon}_{\theta}\left(\mathbf{z}_{t}, \lambda_{t}\right)\) 分贝是带条件和无条件的 \(\boldsymbol{\epsilon}\) 预测值, \(w\) 是指导权重,当\(w=1\) 时,抑制了 classifier-free guidance, 当 \(w>1\) 会增强 guidance 的影响。
进一步可以估计 score: \(\tilde{\boldsymbol{\epsilon}}_{\theta}\left(\mathbf{z}_{t}, \lambda_{t}, \mathbf{c}\right) \approx-\sigma_{t} \nabla_{\mathbf{z}_{t}} \log p\left(\mathbf{z}_{t} \mid \mathbf{c}\right)\),其中 \(p\left(\mathbf{z}_{t} \mid \mathbf{c}\right)\) 是以 \(\mathbf{c}\) 为条件关于 \(\mathbf{z}_{t}\) 的概率密度。
为了从扩散模型中采样,可以从随机噪声 \(\mathbf{z}_{1} \sim \mathcal{N}(\mathbf{0}, \mathbf{I})\) 开始,然后使用 DDIM 方法采样,具体过程为:
-
step1: 由模型得到 \(\epsilon_{\theta}\left(\mathbf{z}_{t}, \lambda_{t}, \mathbf{c}\right)\) 和 \(\epsilon_{\theta}\left(\mathbf{z}_{t}, \lambda_{t}\right)\),进一步得到 \(\tilde{\boldsymbol{\epsilon}}_{\theta}\left(\mathbf{z}_{t}, \lambda_{t}, \mathbf{c}\right)\);
-
step2:根据 \(\mathbf{z}_{t}\) 和 \(\tilde{\boldsymbol{\epsilon}}_{\theta}\left(\mathbf{z}_{t}, \lambda_{t}, \mathbf{c}\right)\) 得到 \(\hat{\mathbf{x}}_{\theta}\left(\mathbf{z}_{t}, \lambda_{t}, \mathbf{c}\right)=\left(\mathbf{z}_{t}-\sigma_{t} \tilde{\epsilon_{\theta}}\left(\mathbf{z}_{t}, \lambda_{t}, \mathbf{c}\right)\right) / \alpha_{t}\) ;
-
step3:估计 \(\mathbf{z}_{s}=\alpha_{s} \hat{\mathbf{x}}_{\theta}\left(\mathbf{z}_{t}, \lambda_{t}, \mathbf{c}\right)+\sigma_{s}\tilde{\epsilon_{\theta}}\left(\mathbf{z}_{t}, \lambda_{t}, \mathbf{c}\right)\)
\(\mathbf{z}_{s}=\alpha_{s} \hat{\mathbf{x}}_{\theta}\left(\mathbf{z}_{t}, \lambda_{t}, \mathbf{c}\right)+\frac{\sigma_{s}}{\sigma_{t}}\left(\mathbf{z}_{t}-\alpha_{t} \hat{\mathbf{x}}_{\theta}\left(\mathbf{z}_{t}, \lambda_{t}, \mathbf{c}\right)\right)\)
式中, \(s<t\) 在 1 到 0 之间取均匀分布序列,最先的采样来自对扩散过程的反转,注意到:
\[q\left(\mathbf{z}_{s} \mid \mathbf{z}_{t}, \mathbf{x}\right)=\mathcal{N}\left(\mathbf{z}_{s} ; \tilde{\boldsymbol{\mu}}_{s \mid t}\left(\mathbf{z}_{t}, \mathbf{x}\right), \tilde{\sigma}_{s \mid t}^{2} \mathbf{I}\right)\]式中, \(\tilde{\boldsymbol{\mu}}_{s \mid t}\left(\mathbf{z}_{t}, \mathbf{x}\right)=e^{\lambda_{t}-\lambda_{s}}\left(\alpha_{s} / \alpha_{t}\right) \mathbf{z}_{t}+\left(1-e^{\lambda_{t}-\lambda_{s}}\right) \alpha_{s} \mathbf{x}\) ,并且 \(\tilde{\sigma}_{s \mid t}^{2}=\left(1-e^{\lambda_{t}-\lambda_{s}}\right) \sigma_{s}^{2}\), 遵循随机更新规则:
\[\mathbf{z}_{s}=\tilde{\boldsymbol{\mu}}_{s \mid t}\left(\mathbf{z}_{t}, \hat{\mathbf{x}}_{\theta}\left(\mathbf{z}_{t}, \lambda_{t}, \mathbf{c}\right)\right)+\sqrt{\left(\tilde{\sigma}_{s \mid t}^{2}\right)^{1-\gamma}\left(\sigma_{t \mid s}^{2}\right)^{\gamma}} \boldsymbol{\epsilon}\]式中, \(\epsilon \sim \mathcal{N}(\mathbf{0}, \mathbf{I})\), 其中 \(\gamma\) 控制采样的随机性。
实施细节
Imagen 的提出的改进主要体现在:
- 引入新的动态阈值技术,这样采样器可以使用非常大的无分类器指导权重;
- 在超分辨率模型中引入噪声增强,提高图像逼真度;
- 引入一种新的高效 U-Net 架构,这种架构具有更高的计算效率、更高的内存效率和更快的收敛速度;
阈值技术
增加 classifier-free guidance 的指导权重可以提高图像-文本的对齐,但会影响图像逼真度,产生高度饱和和不自然的图像。导致这个现象的原因是高指导权重引起训练测试不匹配:在每个采样步 \(t\),\(x\) 的预测值 \(\hat x_0^t\) 必须与训练数据在同一范围内,即在 [−1, 1] 内。但使用高指导权重会使 \(x\) 预测值超出这些界限。这样就导致训练测试不匹配的情形,扩散模型在整个采样过程中会迭代应用自身输出,这样的采样过程会导致产生不自然的图像,有时甚至发散。
为解决上述训练测试不匹配问题,引入了阈值技术:
静态阈值:对 \(x\) 的预测值逐元素裁剪到 [-1, 1] ,称为静态阈值。这样方法对于大引导权重的采样至关重要,并可以防止产生空白图片。尽管如此,随着指导权重的增加,静态阈值处理仍会使图像出现过饱和或细节少的问题,伪代码如下:
def sample():
for t in reversed(range(T)):
# Forward pass to get x0_t from z_t.
x0_t = nn(z_t, t)
# Static thresholding.
x0_t = jnp.clip(x0_t, -1.0, 1.0)
# Sampler step.
z_tm1 = sampler_step(x0_t, z_t, t)
z_t = z_tm1
return x0_t
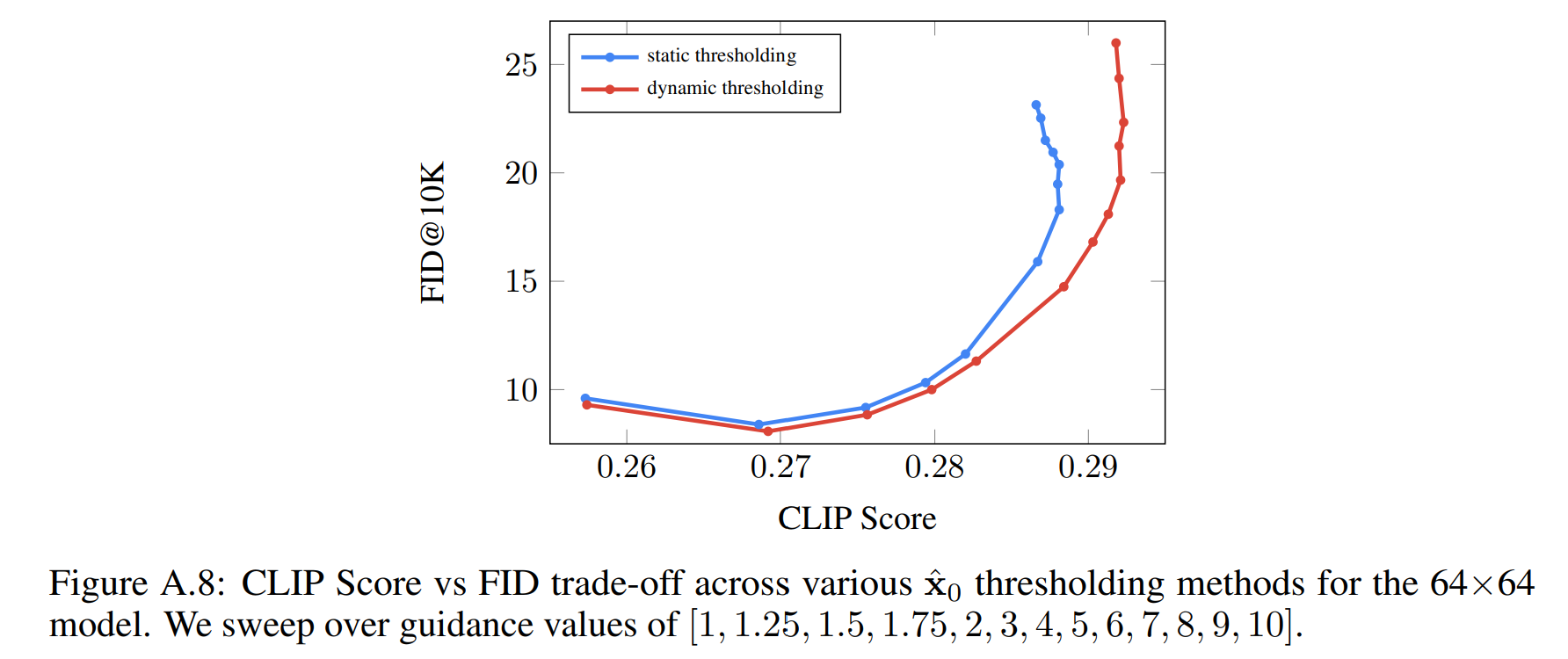
动态阈值:在每个采样步将 \(s\) 设置为 \(\hat x_0^t\) 中的某个百分位绝对像素值,如果 \(s > 1\),那么我们将 \(\hat x^t_0\) 调整到 [−s, s] 范围内,然后除以 \(s\)。动态阈值处理可以推动饱和像素(接近 -1 或 1) 向内收缩,从而主动防止像素在每一步产生饱和。这可显著提高图像的真实感,以及更好的图像文本对齐,尤其是在使用非常大的引导权重时,伪代码如下:
def sample(p: float):
for t in reversed(range(T)):
# Forward pass to get x0_t from z_t.
x0_t = nn(z_t, t)
# Dynamic thresholding (ours).
s = jnp.percentile(jnp.abs(x0_t), p,axis=tuple(range(1, x0_t.ndim)))
s = jnp.max(s, 1.0)
x0_t = jnp.clip(x0_t, -s, s) / s
# Sampler step.
z_tm1 = sampler_step(x0_t, z_t, t)
z_t = z_tm1
return x0_t

噪声增强
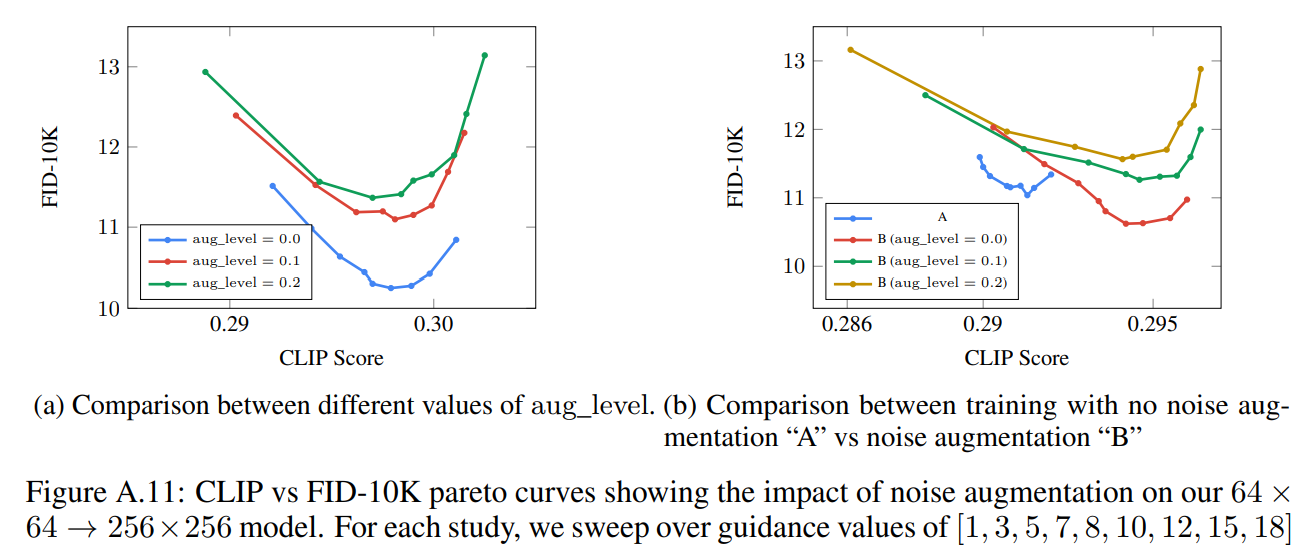
Imagen 利用一个 64×64 base 模型,和两个文本条件超分辨率扩散模型,分别将生成的 64 × 64 图像上采样到 256 × 256 ,然后再上采样到 1024 × 1024 。 Imagen 对两个超分辨率模型都使用噪声调节增强 ,这对于生成高逼真度的图像至关重要。
训练时随机选择 aug_level ,推理时,选择比较不同的 aug_level 以找到最佳的样本质量。增强级别的范围 aug_level ∈ [0, 1] ,在实践中 aug_level 取 [0.1, 0.3] 的 会取得更好的效果,伪代码如下:
训练过程:
def train_step(
x_lr: jnp.ndarray, x_hr: jnp.ndarray):
# Add augmentation to the low-resolution image.
aug_level = jnp.random.uniform(0.0, 1.0)
x_lr = apply_aug(x_lr, aug_level)
# Diffusion forward process.
t = jnp.random.uniform(0.0, 1.0)
z_t = forward_process(x_hr, t)
Optimize loss(x_hr, nn(z_t, x_lr, t, aug_level))
采样过程:
def sample(aug_level: float, x_lr: jnp.ndarray):
# Add augmentation to the low-resolution image.
x_lr = apply_aug(x_lr, aug_level)
for t in reversed(range(T)):
x_hr_t = nn(z_t, x_lr, t, aug_level)
# Sampler step.
z_tm1 = sampler_step(x_hr_t, z_t, t)
z_t = z_tm1
return x_hr_t

网络架构
Base 模型: 64 × 64 文本到图像 base 扩散模型使用 3 中的 U-Net 架构,调整点:(1)在整个文本嵌入序列的多个分辨率上添加交叉注意力;(2)在注意力和池化层的文本嵌入做层归一化。
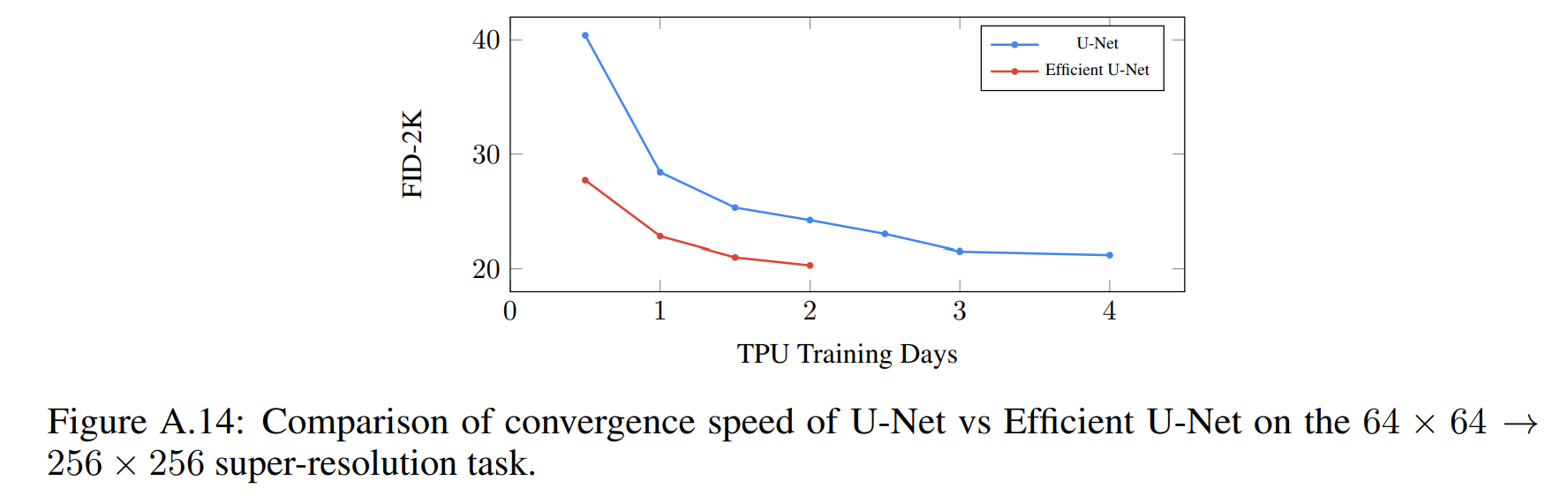
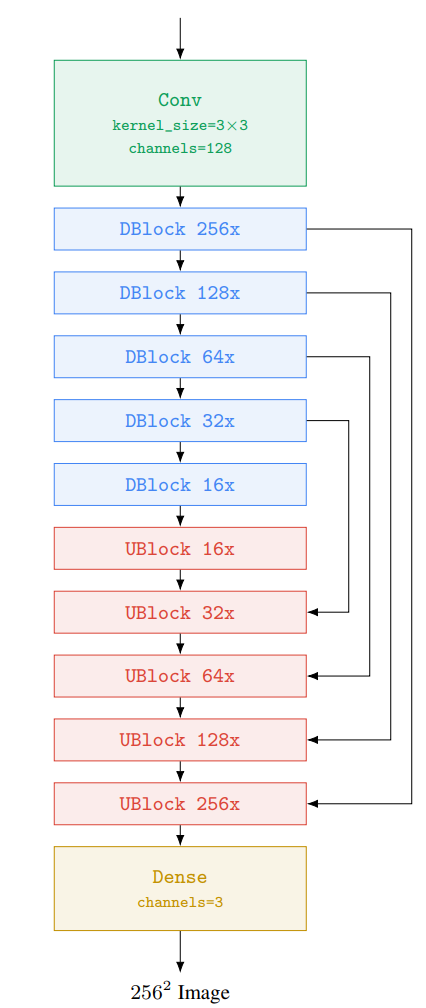
超分辨率模型:对于 64 × 64 → 256 × 256→ 1024 × 1024 的超分辨率模型,所使用的 U-Net 模型改编自 [40, 58]。为了提高记忆力效率、推理时间和收敛速度,对 U-Net 做了调整,称做 Efficient U-Net 。调整点:移除 self-attention 层,保留文本 cross-attention 层。在 64 × 64 → 256 × 256 的超分辨率任务上,U-Net 和 Efficient U-Net 的性能对比如下图,可以看出 Efficient U-Net 的收敛速度明显快于 U-Net, 并且可以获得更好的性能,此外 Efficient U-Net 在采样速度上也可以加快 ×2 − 3 倍。
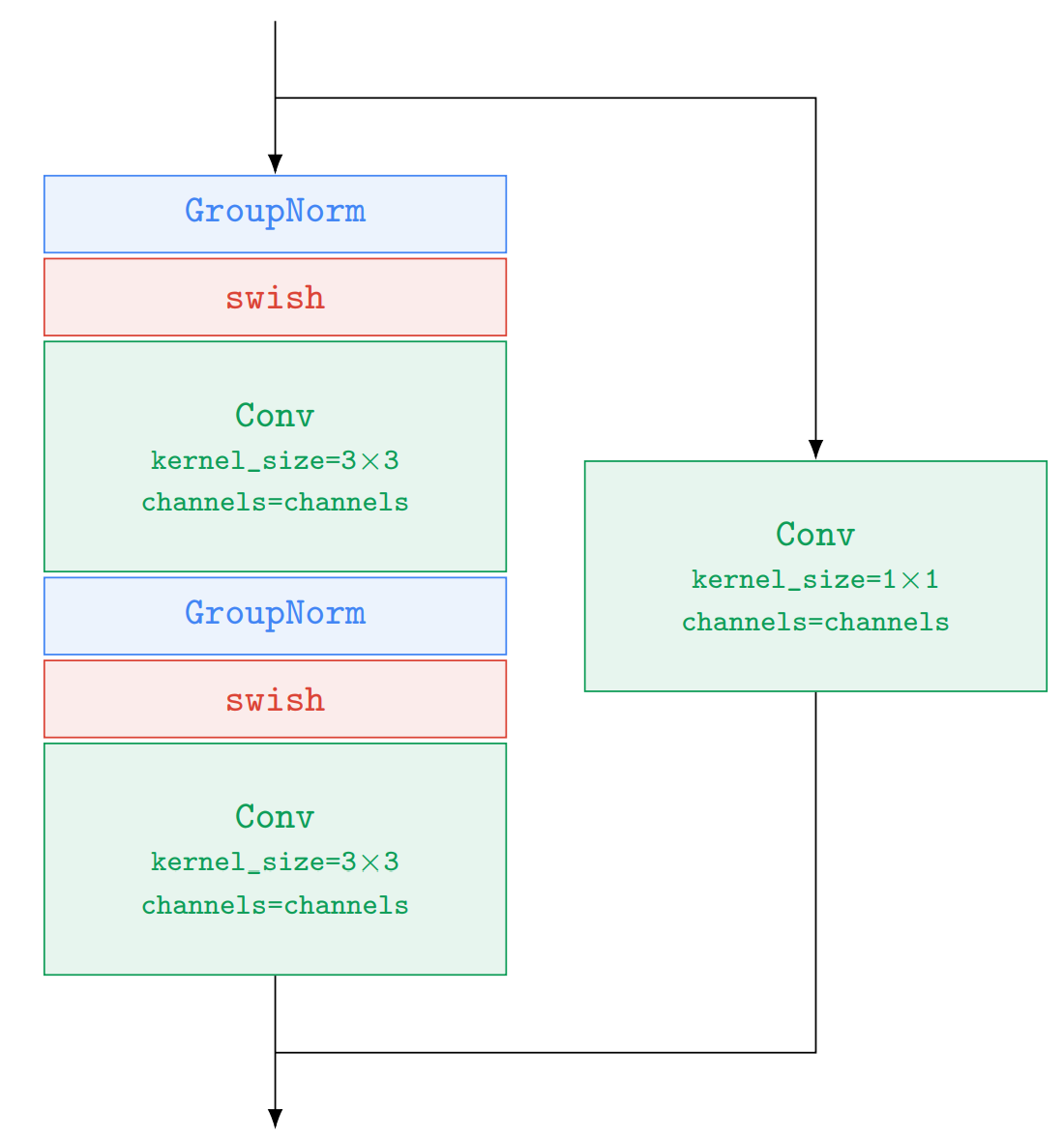
ResNetBlock 在 DBlock 和 UBlock 都会被使用,ResNetBlock 的 超参数是 channels 数。
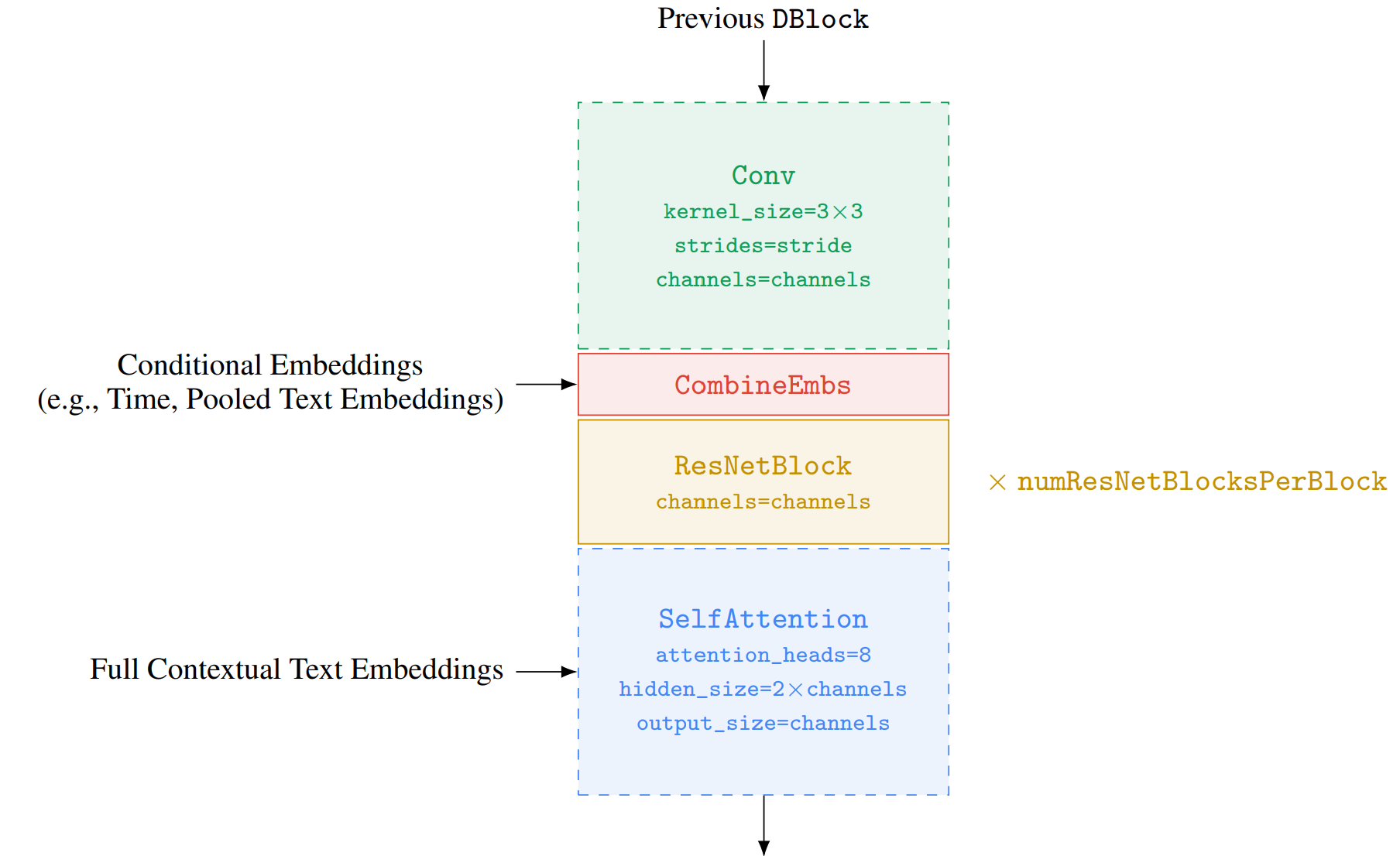
DBlock 的超参数是:下采样步长 stride: Optional [Tuple[int, int]],每个 DBlock 的 ResNetBlock 数量 numResNetBlocksPerBlock:int,通道数 channels:int, 虚线块是可选的,例如,并非每个 DBlock 都需要下采样或需要自注意。
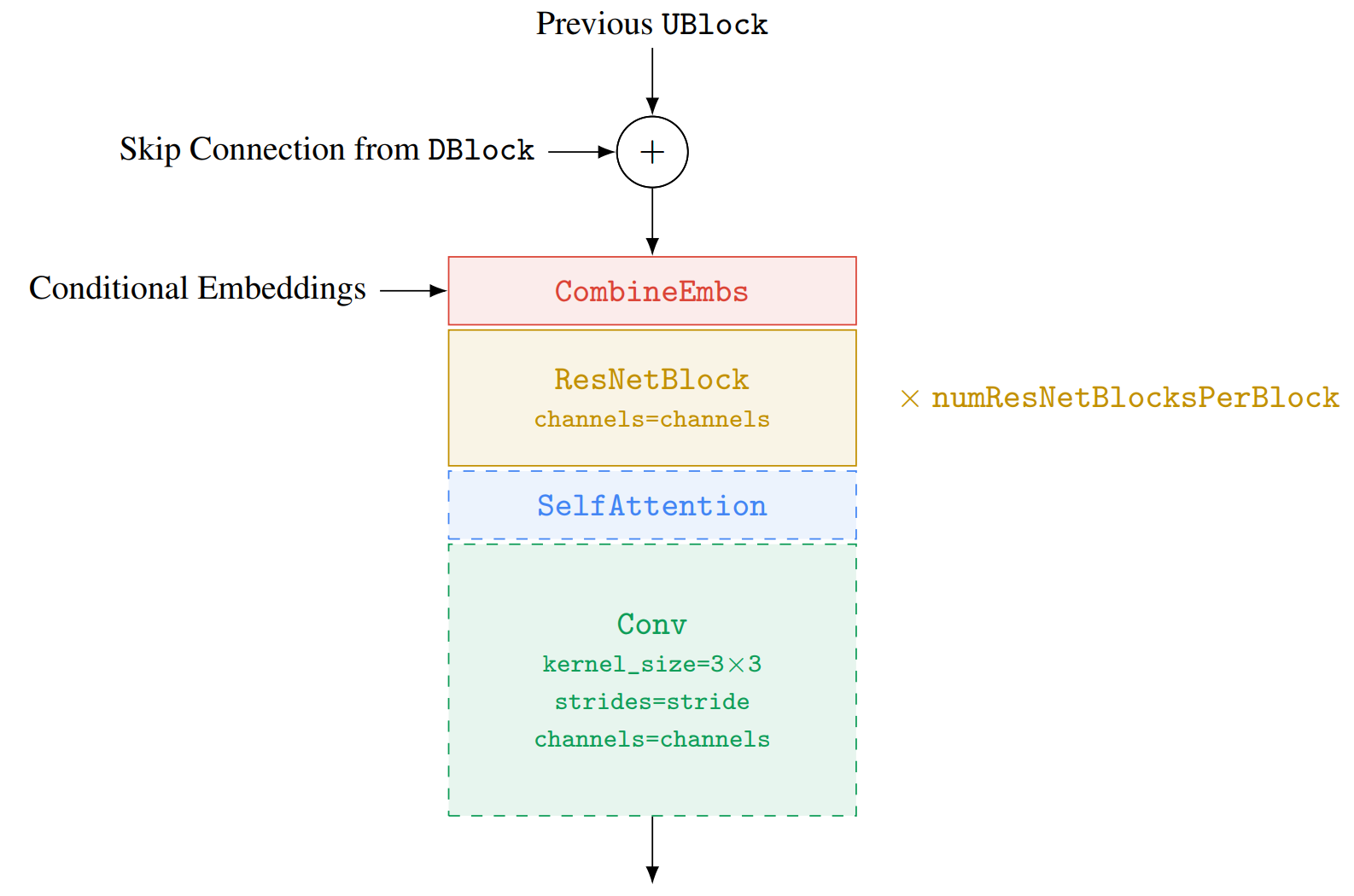
UBlock 的超参数是:上采样步长 stride: Optional[Tuple[int, int]],每个 DBlock 的 ResNetBlock 数量 numResNetBlocksPerBlock:int,通道数 channels:int, 虚线块是可选的。
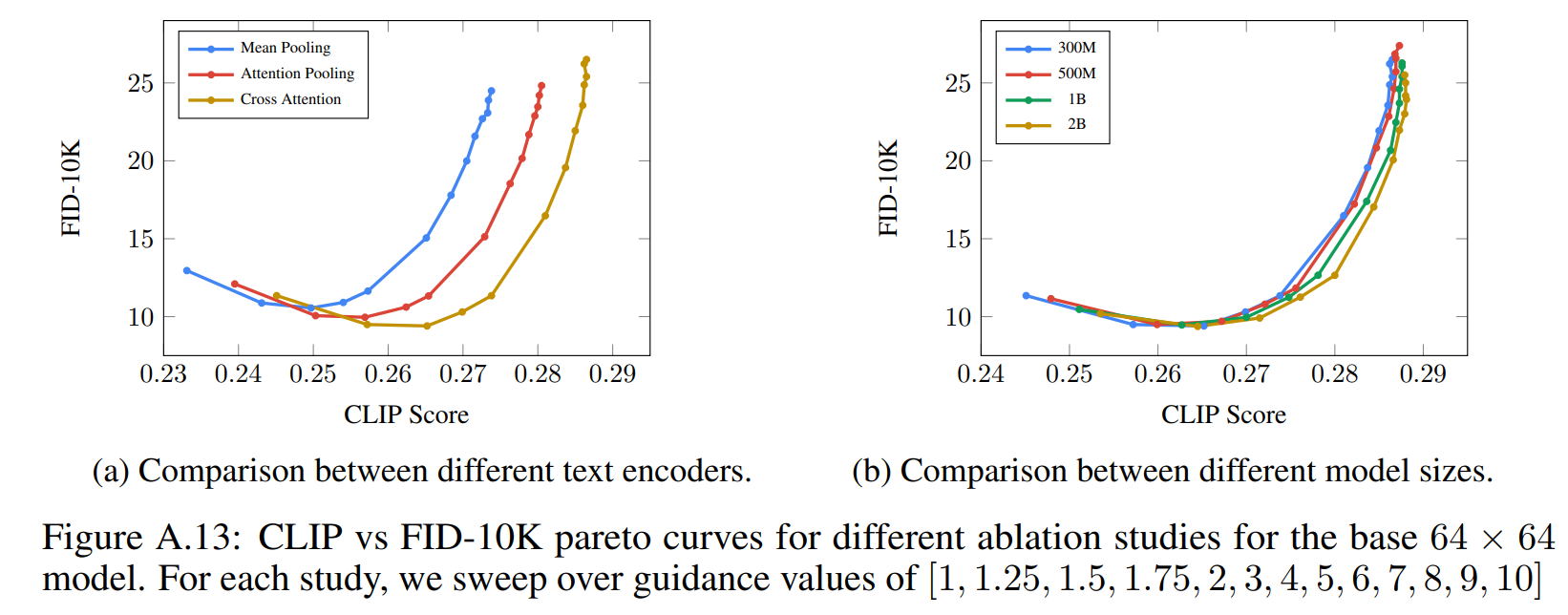
文本嵌入和模型尺寸:图 A.13a 比较了对文本嵌入进行平均池化、注意力池化和交叉注意力的性能,使用交叉注意力可以取得更好的性能。图 A.13b 绘制了 64 × 64 各种 U-Net 模型大小的 CLIP-FID 得分权衡曲线。 随着模型的增大,可以获得更好的权衡曲线;另外,增大文本编码器模型相比 U-Net 模型,会产生更好的结果。