深入理解 DALL-E

DALL-E 可以让模型生成与给定文本提示相匹配的图像，当模型被要求生成 “鳄梨形状的扶手椅” 图像时，它能够生成超级有创意的鳄梨椅设计，博客参考¹。

除了创造性设计之外，transformer 似乎还了解一些常识性物理学。 例如，要求生成 “戴着耳机的熊猫宝宝盯着镜子里的倒影”，会产生下图结果，生成的结果中甚至有镜子反射的物理细节。

此外，DALL-E 似乎也包含了关于我们世界的知识。 例如要求生成 “旧金山阿拉莫广场在晚上的街道上的照片”， 会产生下图结果：

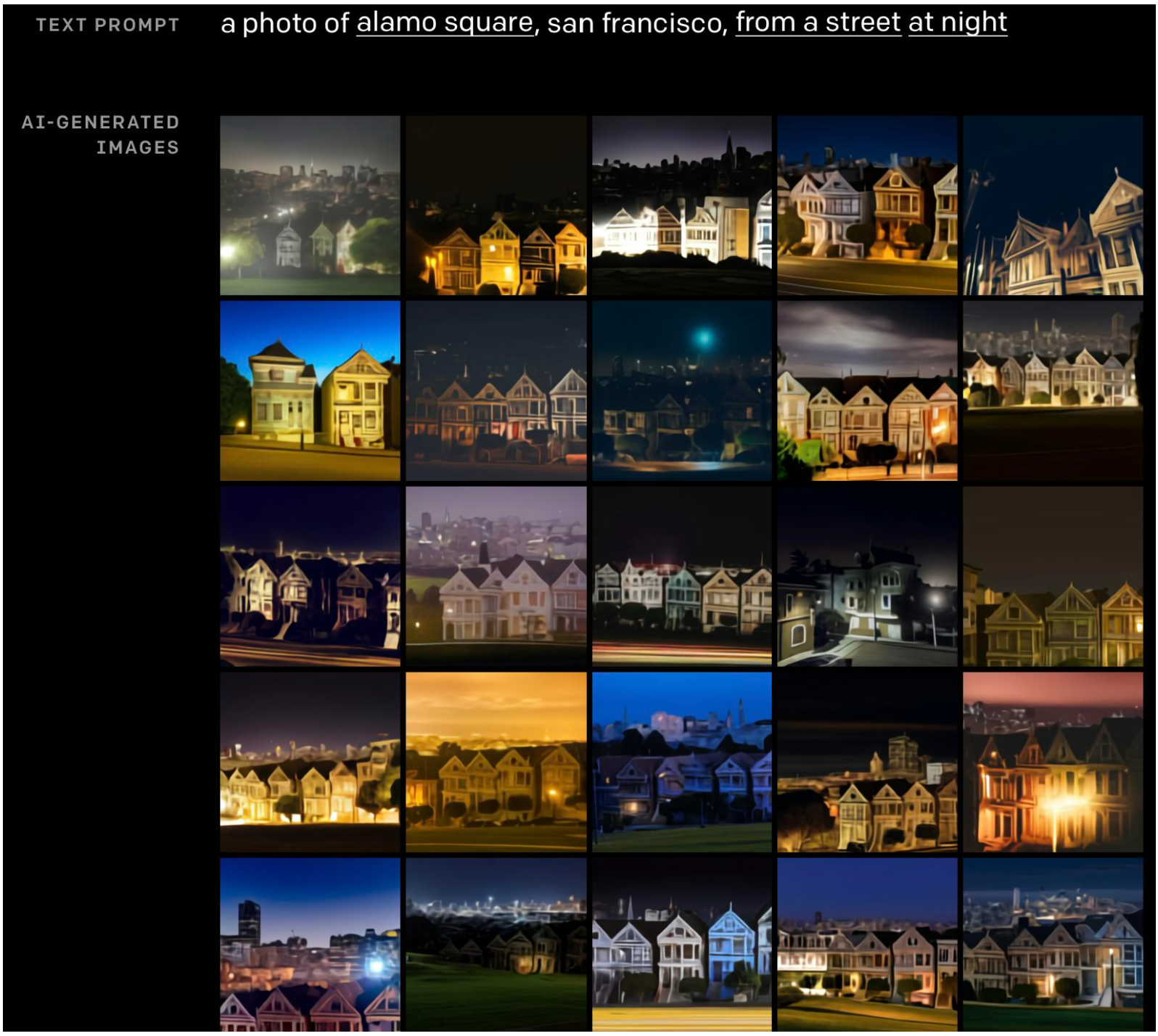
在 OpenAI 的博客 中还有很多类似令人印象深刻的例子（遗憾的是模型没有发布，所以我们无法自己测试这些例子）。

我们不免产生一个疑问：它怎么这么好？

没有人确切地知道为什么它会工作得这么好，甚至没有人知道他们实际学到了什么；没有深度学习的基本理论可以解释所有这些，目前来说，这些网络对于我们太大太复杂，无法完全理解。我们所知道的只是这些疯狂的结果，所以“它怎么这么好？”是一个开放的研究问题。

尽管如此，还是有一些普遍的直觉可以帮助理解这些模型的能力和局限性。 为了探索“它怎么这么好？”这个问题，下面的博客将分为两个不同的部分：

• 前半部分重点介绍 DALL-E 的不同部分如何组合在一起，以从文本提示中生成高质量图像。特别是，本节将着眼于 transformers 在这些方面所扮演的角色。
• 在了解 transformers 如何融入 DALL-E 架构的基础上，将关注 transformers 功能的更多哲学问题，例如“它怎么这么好？”以及“为什么 transformers 能够做到这一切？” 在这一部分中，我将较少关注 transformers 的技术细节，实际上已经有很多很棒的博客详细地涵盖了这个主题。我可以推荐 Jay Allamar 的 博客，以及哈佛 NLP 的 annotated transformer。 我也不会试图明确地回答这些问题，因为这些都是开放的研究问题，没有人真正知道问题答案，相反，我只会提出一些有趣的直觉，让我们更清楚地了解这些模型可以做什么，以及是怎样做到的。

这篇博文假设您对深度学习和贝叶斯概率有一定的了解。

D-VAE的理解

在之前博客²中分析了自编码器。 具体来说，我们探讨了一种特别强大的技术，称为 VQ-VAE。 DALL-E 使用了一种稍微不同的方法来学习图像的离散表示，称为 D-VAE。 虽然与 VQ-VAE 稍有不同，但核心目标是一致的。

VQ-VAE 回顾

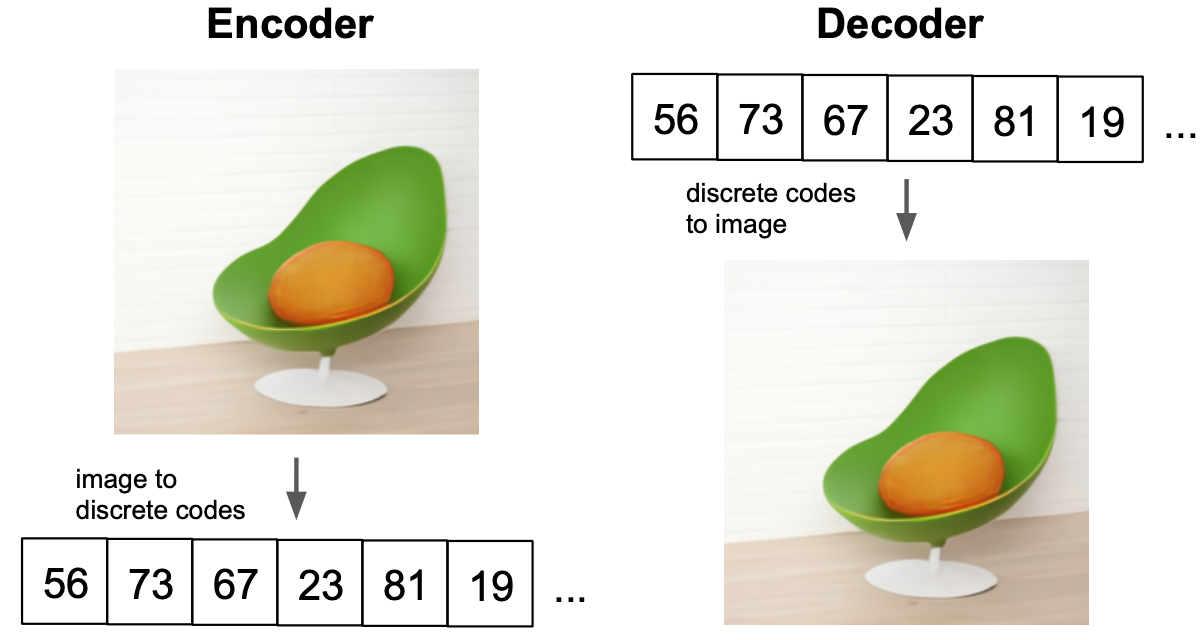
回顾 VQ-VAE 学习 codebook, 一组有限的关于学习向量的可索引查找表格。 encoder 负责接收图像并输出一组向量，每个向量在理想状态下接近某个 codebook 向量。

encoder 输出的尺寸比原始图像小很多， 因为这里目标是强制模型压缩图像，以便它学习更基本的图像表示，只突出最重要的特征。

在 encoder 产生一组输出后，VQ-VAE bottleneck 将每个编码器输出向量映射到距离其最近的 codebook 向量。 最后，这些 codebook 向量被送到 decoder，其任务是重建原始图像。

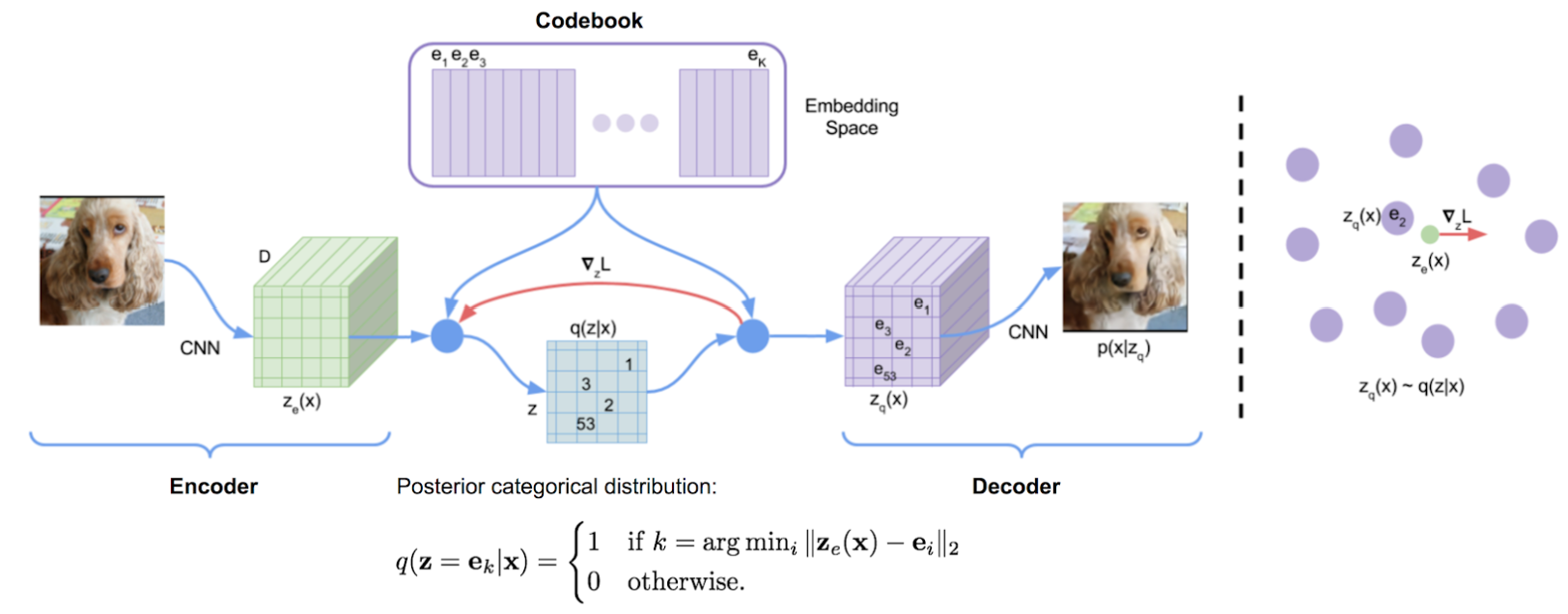
如果我们只是用标准的 VAE 目标训练这个模型，是行不通的。必须采用一些额外的向量量化技巧，以便能够通过 bottleneck 进行反向传播，并对齐 encoder 向量与 codebook 向量。

从根本上说，这些技巧之所以必要，是因为模型假设 \(z=\text{argmin}_{i}\Vert z_e(x)-e_i\Vert_2\)，则 \(q(z\mid x)=1\)，否则\(q(z\mid x)=0\)，这里 \(x\) 是输入图像，\(q(z\mid x)\) 是给定图像的隐变量向量分布，\(z_e(x)\) 是给定图像的 encoder 输出向量，\(e_i\) 是 codebook 向量的集合。基本上这个方程是说 VAE 的后验分布是确定性的，最接近 encoder 输出的 codebook 向量概率设为1。

不确定性后验

不过，后验分布通常不需要是确定性的。实际上，您可以想象 encoder 可能不确定要输出哪个 codebook 向量。 VQ-VAE 强制模型在所有情况下只选择一个向量，但 encoder 最好在后验分布中表达一些隐变量的不确定性，这就是 D-VAE 所做的。

D-VAE 编码器仍会为给定图像输出一些离散的隐变量网格。但是，D-VAE 编码器不是生成每个都确定性地映射到codebook 向量的隐变量，而是为每个隐变量输出在 codebook 向量上的分布。

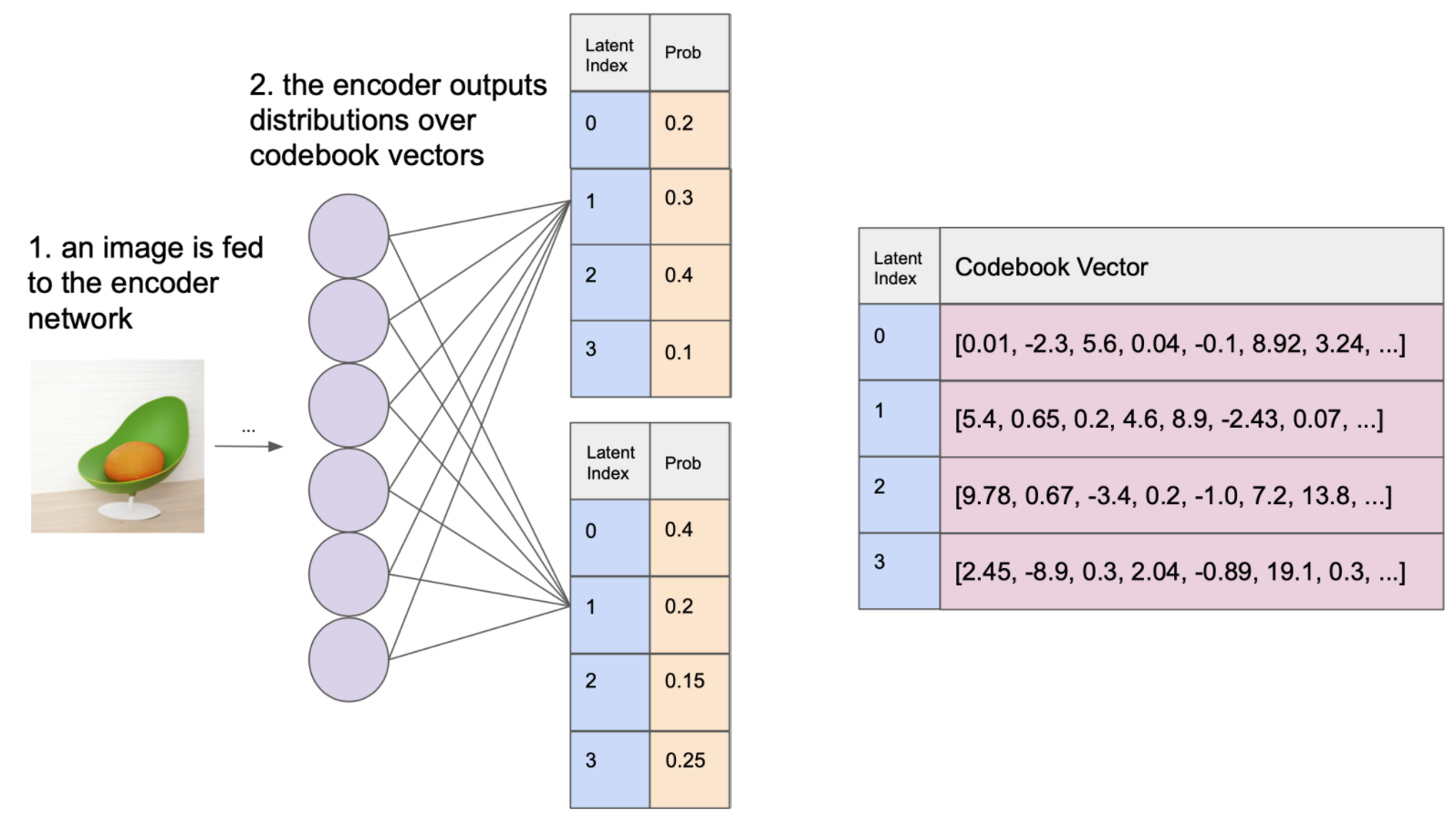
离散问题

现在我们只需要从这每一个分布中采样 codebook 向量，然后我们只需将它们提供给解码器。 这很容易，对吧？ 嗯，这个过程实际上有一个大问题：你不能通过从分类分布中采样进行反向传播。

一般来说，深度学习不能很好地处理离散问题。 VQ-VAE 解决了这个问题，提出了一套很好的矢量量化的技巧， D-VAE 则使用了一个非常不同的技巧。

为了解决离散采样问题，D-VAE 放宽了 bottleneck，允许它在 codebook 向量集的凸包中的任何位置输出向量。 可以通过超参数 \(\tau\) 调整这种放宽，当 \(\tau \rightarrow 0\) ，则接近离散采样，在训练过程中对 \(\tau\) 进行退火，该模型能够有效地从离散的隐变量分布中学习。

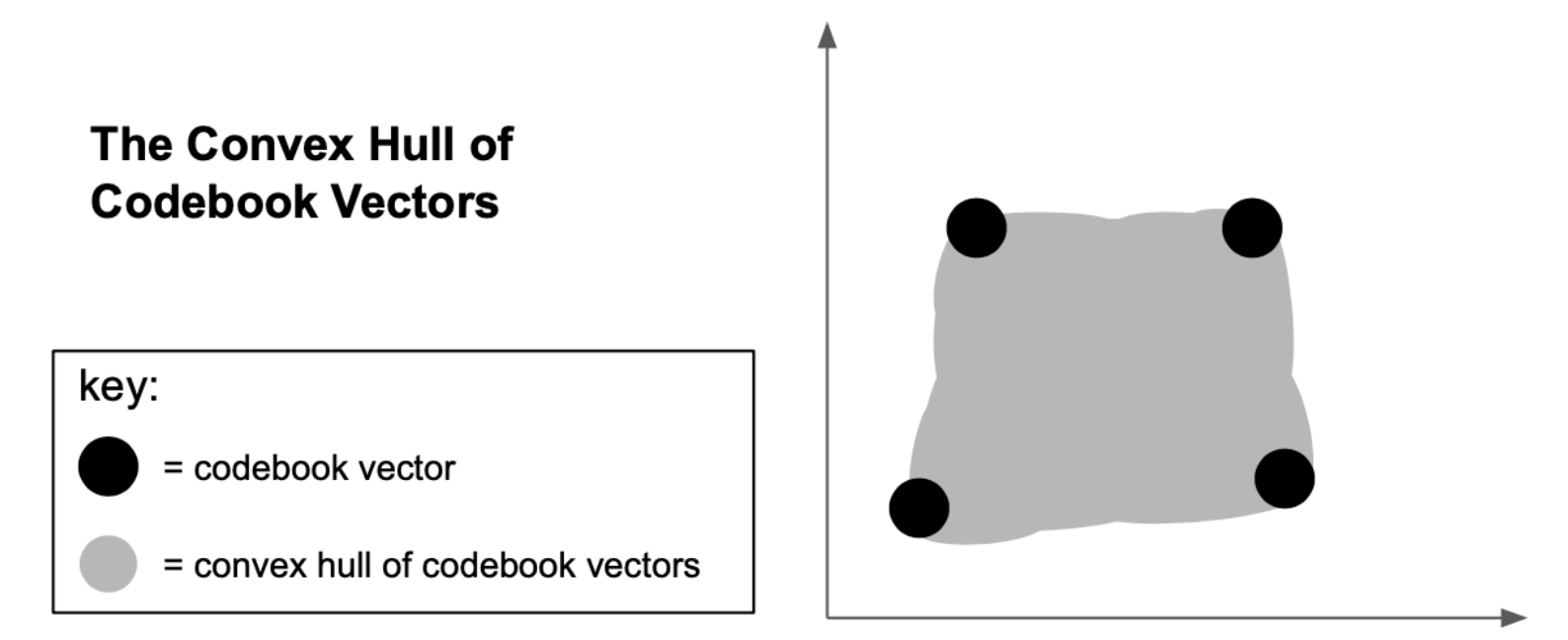
Gumbel Softmax 松弛

D-VAE 使用的特定放宽称为 Gumbel Softmax 松弛。我认为这是解决此问题的一个很好的方案，让我们深入研究细节。 回想一下，我们在 codebook 向量集上( 有 \(k\) 个向量) 的分布是 \(q(e_i\mid x)\) ，其中 \(e_i\) 是第 \(i\) 个 codebook 向量。从这个分布中采样隐变量的一种方法是：

\[z = \text{codebook}[\text{argmax}_i[g_i + log(q(e_i\mid x))]]\]

式中 \(g_i\) 是来自 Gumbel 分布 的独立样本，\(\text{codebook}[i]\) 是在第 \(i\) 个索引位置查找到的向量 codebook。

我们无法对 \(\text{argmax}\) 微分，因此 Gumbel softmax 松弛将 \(\text{argmax}\) 替换为 \(\text{softmax}\)。这样从 \(\text{softmax}\) 采样将在 codebook 向量集上产生一组权重 \(y_i\)：

\[y_i = \frac{e^{\frac{g_i + log(q(e_i\mid x))}{\tau}}}{\sum_{j=1}^{k} e^{\frac{g_j + log(q(e_j\mid x))}{\tau}}}\]

采样的隐向量是这些 codebook 向量的加权和：

\[z = \sum_{j=1}^k y_je_j\]

现在我们可以通过关于编码器输出的采样操作 \(q(e_i\mid x)\) 来做微分，这是因为:

• 这个新方程在任何地方都是可微的。

• 随机采样来自 \(g_i\)：一个独立于我们编码器输出的外部变量。

这种根据外部变量参数化随机样本的方法称为重参数化技巧 (reparameterization trick)。该技巧不适用于离散分布，因此我们必须将原始分类分布转换为连续分布才能使其起作用。

这种连续分布与我们最初的分类分布有何相似之处？

注意到超参数 \(\tau\) 在 Gumbel Softmax 公式中的作用，随着该参数接近零，权重 \(y_i\) 在最大值 \(g_i + log(q(e_i\mid x))\) 附近变得越来越尖锐，最终逼近设定的 one-hot argmax 权重，这将等价于分类分布：

\[z = \text{codebook}[\text{argmax} _i[g_i + log(q(e_i\mid x))]]\]

另一方面，对于较大的 \(\tau\) 值，Gumbel softmax 将接近确定性分布，这将 codebook 向量集的质心样本概率设置为1。

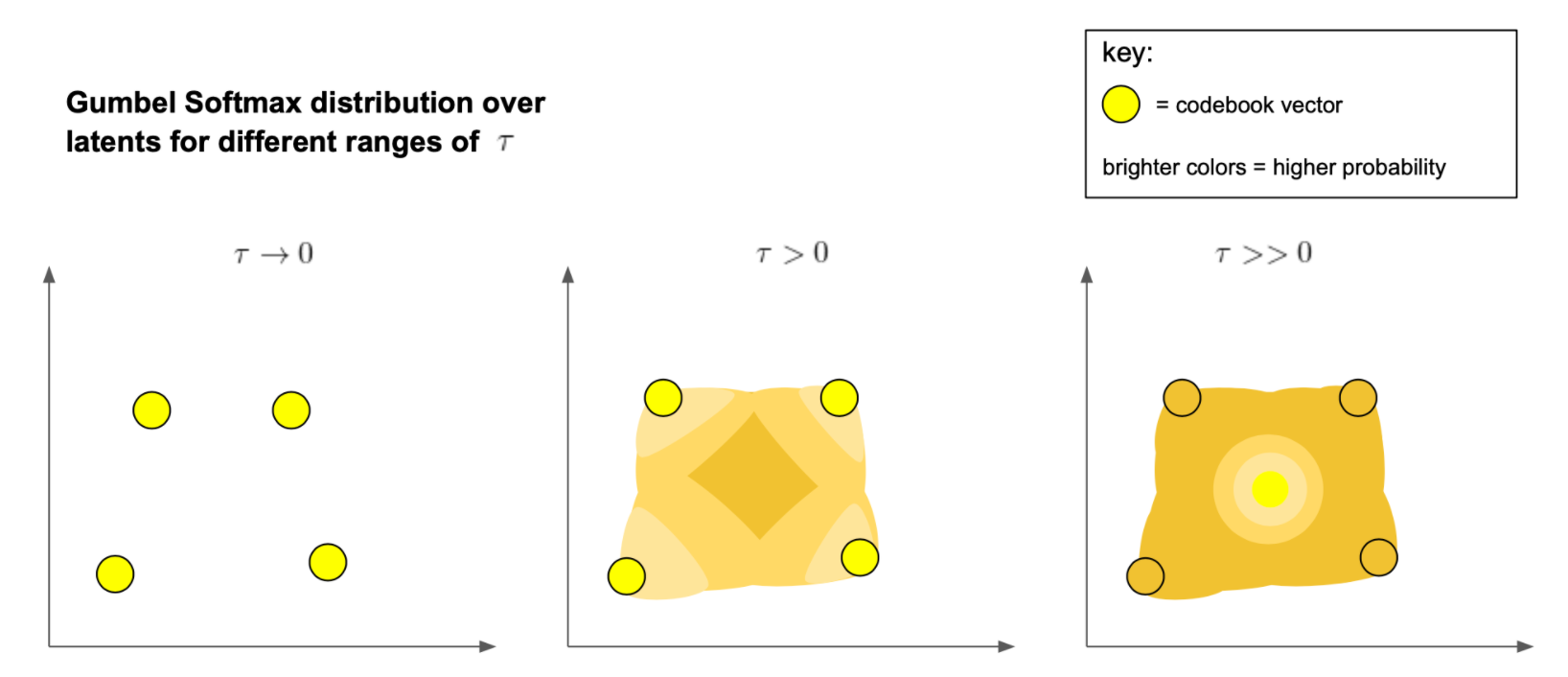
Putting It All Together

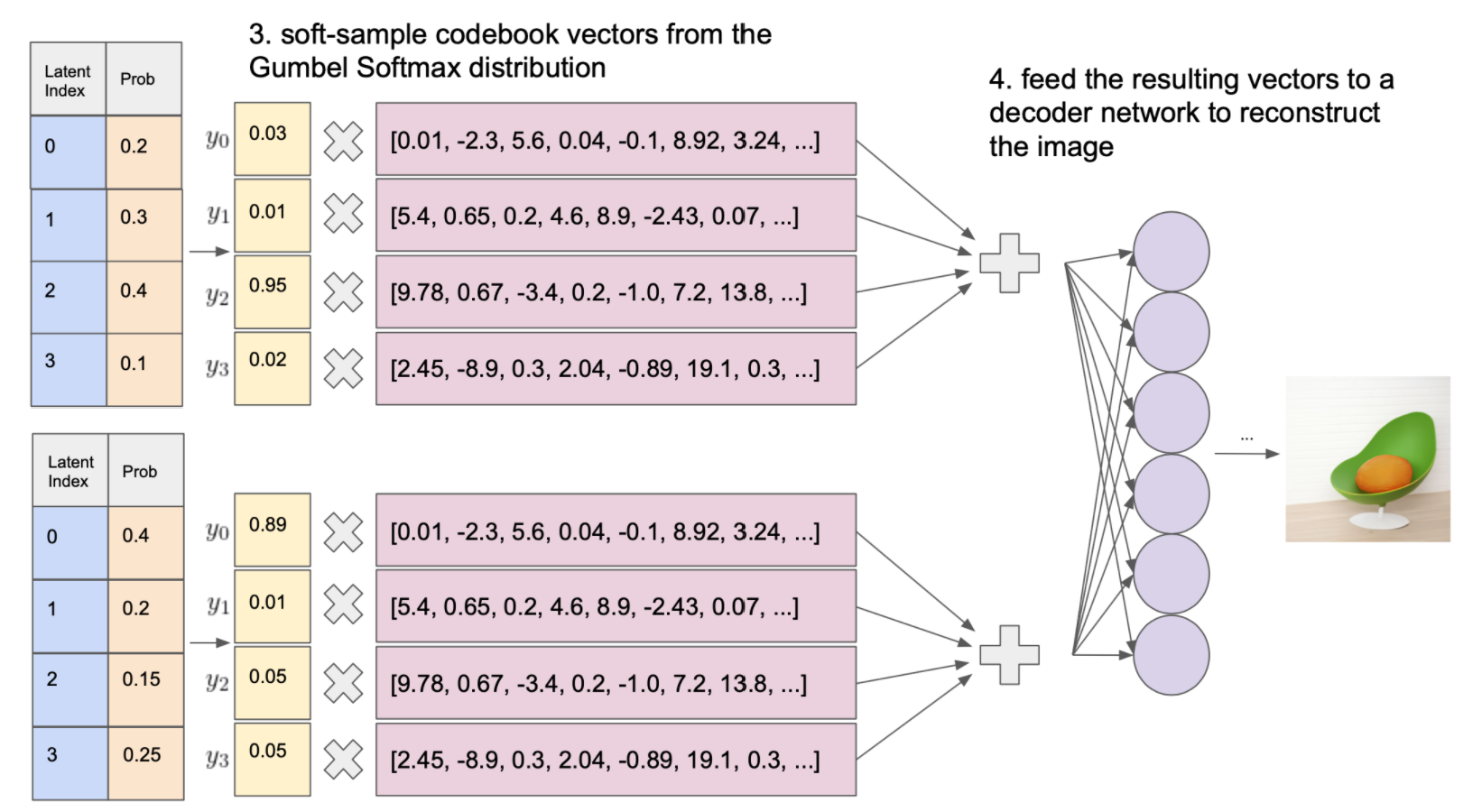
现在我们可以对 D-VAE 的 bottleneck 做微分，重建图像只涉及两个步骤：

1. 来自松弛后验的样本 codebook 向量。
2. 将这些向量输入给 decoder 网络， decoder 将尽可能地重建输入，就像在 VQ-VAE 中那样。

为了训练模型，我们只需最小化标准 VAE 目标（ ELBO）：

\[-E_{z \sim q(z\mid x)}[log(p(x\mid z))]+KL(q(z|x) \Vert p(z))\]

这里 \(p(x\mid z)\) 是解码器对图像的重建，样本 \(z \sim q(z\mid x)\) 取自 Gumbel softmax 松弛。

\(p(z)\) 是隐变量的先验，初始化为所有 codebook 向量的均匀分布。正如我们将在下一节中看到的，DALL-E 训练的第二阶段涉及使用 transformer 模型更新此先验，最终进一步最小化此损失函数。

总体而言，D-VAE 与 VQ-VAE 具有相同的目标：它们都试图学习复杂数据分布的离散隐变量表示，例如自然图像的分布。 不过，每种方法都以自己独特的方式解决问题。 VQ-VAE 使用矢量量化，而 D-VAE 将离散采样问题放宽为连续近似。 尽管每种技术都有自己的权衡取舍，但最终它们都同样有效。

DALL-E：大图景

现在我们了解了 DALL-E 的自编码器背后的具体细节，让我们后退一步，看看更大的图景，以便我们更好地了解 DALL-E 的 transformer 在其架构中所扮演的确切角色。

DALL-E 的最终目标是学习给定文本字符串的图像的条件分布，即 \(p(x\mid y)\)，其中 \(x\) 是图像，\(y\) 是文本提示。

（DALL-E 实际上更进一步，计算文本和图像之间的联合分布，但为简单起见，我们只考虑条件分布。）

一旦我们学习到了这种分布，我们就可以输入一些文本提示，例如“鳄梨形状的扶手椅”，然后通过 \(p(x\mid y)\) 采样来生成各种图像。

但这种采样是如何起作用的呢？我们首先应该如何学习 \(p(x\mid y)\)？

第一个问题实际上取决于我们选择学习的 \(p(x\mid y)\) 的因式分解。因此，如果不形成解决第二个问题的方法，我们就无法真正回答第一个问题。

那么……我们应该如何学习 \(p(x\mid y)\)？

首先，我们需要一个巨大的自然文本图像对数据集； 针对于此，DALL-E 专门从互联网上抓取了 2.5 亿文本图像对进行训练，现在我们只需要训练一个巨大的模型来预测给定文本提示的图像。

实做问题

这一切听起来十分容易，但要让它真正发挥作用，存在许多挑战：

首先 DALL-E 有120亿个参数； 这个模型十分巨大。 很少有公司能负担得起训练这样的模型所需的计算资源，DALL-E 论文 的很大一部分在描述所使用到的分布式训练技巧。

其次，从文本中预测图像的简单方法是不切实际的， 考虑完成此任务的最简单方法：

• step1：将文本 tokens 与相应图像中展开的像素值拼接起来（通常从左上角展开到右下角）。
• step2：给定这个文本和像素值序列，我们可以自回归的方式分解分布 \(p(x\mid y)\)： \(p(x\mid y) = p(x_1, x_2, x_3, ...\mid y)=p(x_1\mid y)p(x_2\mid x_1,y)p(x_3\mid x_1,x_2,y)...\) ，这里 \(x_i\) 是展开图像中的第 \(i\) 个像素值。
• step3：通过任意的自回归序列模型（例如 LSTM 或 Transformer），使用最大似然估计来预测\(p(x_i\mid x_{i-1},x_{i-2},...,x_2,x_1,y)\) 因子，进而估计出 \(p(x\mid y)\)。也就是说，给定一些文本和所有先前的像素值，我们要训练一个模型来预测图像中的下一个像素值。

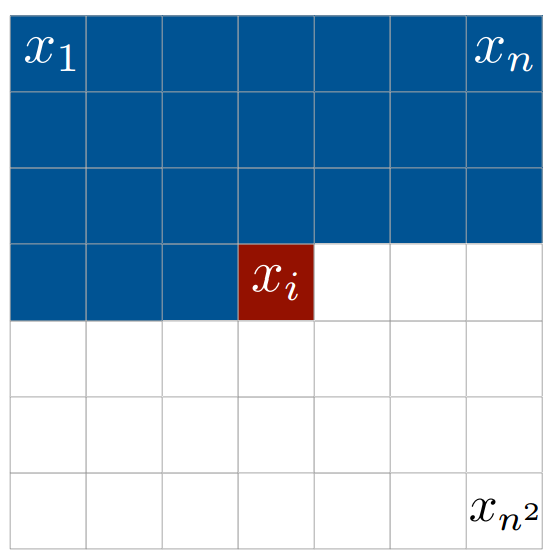
从理论上讲，这种方法非常简单。但我们刚刚描述的方法不切实际，因为 DALL-E 可以处理高分辨率 256x256 RGB 图像。如果这些图像中的像素太多，几乎任何传统的序列模型都无法合理学习。

由于 DALL-E 最多接受 256 个文本 tokens，因此生成的文本和像素序列的总长度将达到 196,864 。任何合理大小的 RNN 或 LSTM 都会忘记该序列中的大部分早期信息，如果您尝试将这么长的序列提供给 transformer，您肯定会遇到 cuda 内存不足的错误，这是因为内存复杂度为\(\mathcal{O}(n^2)\) 。

如果 transformer 可以接受这么长的序列，那么该模型在这个问题上可能会做得很好，甚至可能比 DALL-E 更好，但它需要比 DALL-E 使用的更多的计算资源（DALL-E 已经很多了）。

DALL-E 分解

显然需要一个更聪明的解决方案。我们不是对 \(p(x\mid y)\) 自回归建模，而是根据 D-VAE 的 32x32 压缩的离散图像隐变量网格来分解分布，这种分解为：

\[p(x,z\mid y)=p(x\mid z,y)p(z\mid y)\]

式中，第一项 \(p(x\mid z,y)\) 由 D-VAE 处理，第二项 \(p(z\mid y)\)由 transformer 自回归建模。展开后，我们的隐变量 \(z\) 网格构成长度为 1024 的序列，这是 transformer 建模的合理长度。

DALL-E 正是这样做的，它不是学习预测图像中的每个像素，而是预测图像隐变量序列，然后由 D-VAE 解码器将其转换为高质量图像，这种方法不仅使建模更加实用，也可能给模型带来了一些很好的归纳偏置，其通过允许 transformer 在隐空间中建模，不必专注于图像的细小高频的细节，而是着力于图像大画面上，让 D-VAE 处理较小的细节。

所以，我们可以将 transformer 视为学习描绘大局，这就像有远见的艺术家。而 D-VAE 更像是高清的图像处理软件负责将这种视觉呈现。

尽管这种分解在技术上会导致 \(p(x,z\mid y)\) 而不是 \(p(x\mid y)\)，可以证明在 VAE 目标中对第一个优化等效于对第二个优化：

\[-E_{z \sim q(z\mid x)}[log(p(x\mid z))]+KL(q(z\mid x) \Vert p(z\mid y))\]

分布 \(q(z\mid x,y)\)和 \(p(x\mid y,z)\) 分别由 D-VAE 的编码器和解码器网络建模。而 transformer 模型 \(p(z\mid y)\) 可以结合文本和图像。

D-VAE 和 Transformer 训练都最大限度地减小了这种损失，可以将其视为具有两个独立阶段的训练过程：

• D-VAE 被训练最小化这种损失，其中 \(p(z \mid y)\)设置为均匀分布；

• D-VAE 网络被冻结，通过 Transformer 的最大似然估计来学习 \(p(z\mid y)\)，从而进一步最小化这种损失。

在 DALL-E 论文中，他们提到在早期实验中，同时训练变压器和 D-VAE（即没有对 \(p(z\mid y)\) 做出均匀分布假设），但他们声称这样做并没有提高性能。

DALL-E 采样

现在我们知道了 DALL-E 是如何训练的，以及如何分解 \(p(x\mid y)\) ，我们可以看看怎样使用训练好的 DALL-E 模型采样图像。做法很简单： 假设我们要求模型生成 “鳄梨形状的扶手椅” 的图像。 首先，我们将单词序列“鳄梨形状的扶手椅”输入到 transformer 中，然后以自回归方式从 transformer 中采样后续的图像隐变量序列， 这看起来像：

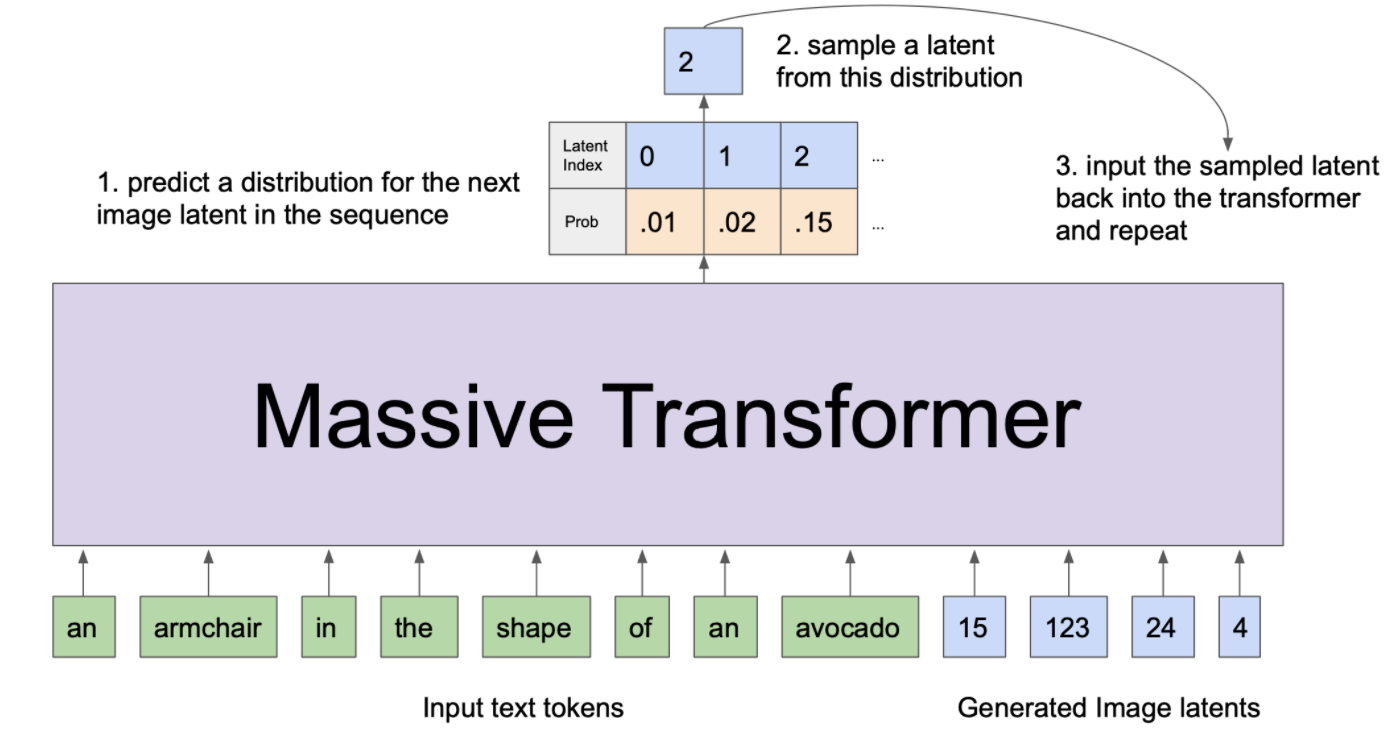
为了渲染从这个生成的隐变量序列中得到的图像，我们只需获取与每个离散隐变量相关的 D-VAE codebook 向量，并将它们提供给 D-VAE 解码器， 这将使我们得到高清的鳄梨椅！

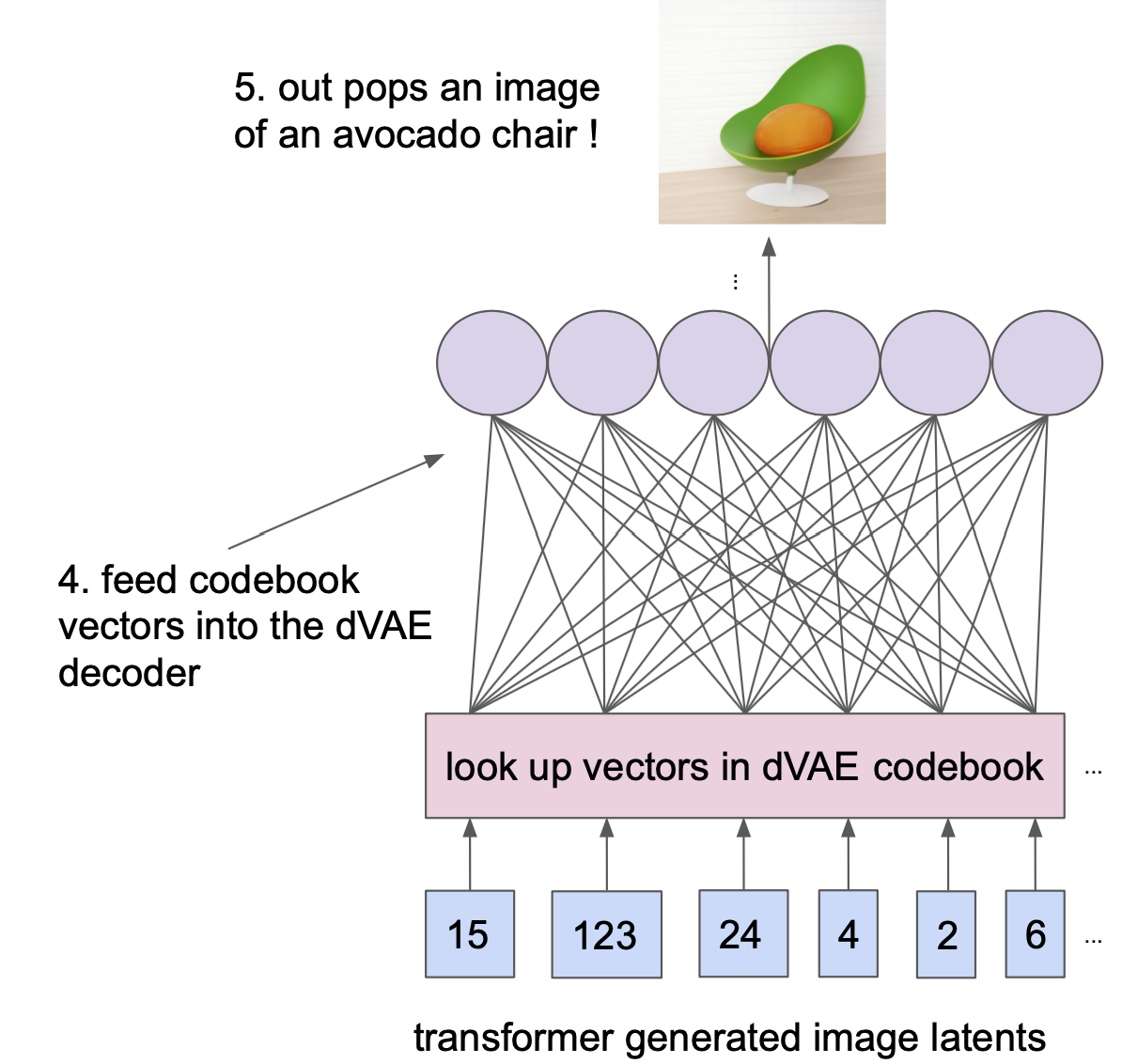
目前基本完成了我们对 DALL-E 背后的建模细节的描述，如果你的后院碰巧有一个巨大的 GPU 农场，并且可以访问包含 2.5 亿个自然文本-图像对的数据集，你可以在这个周末回家训练你自己的 DALL-E 模型（或者实际上，这可能需要几周的训练，不知道你家里有多少 GPU）。

关于 DALL-E 中的 transformers 详细分析请参见下篇博客。

参考