深入理解 VQ-VAE

DALL-E¹ 取得了令人印象深刻的结果，该模型能够根据文本描述生成精确，高质量的图像。它甚至可以产生现实世界中可能不存在的物体渲染，例如“鳄梨形状的扶手椅”。本文将介绍 VQ-VAE²，这是 DALL-E 生成如此多样化和高质量图像分布的关键组件，博客参考³。

基础概念

VQ-VAE 表示 Vector Quantized 变分自编码器，这里涉及到很多内容，我们将首先厘清隐空间 、自编码器以及变分自编码器的基础概念。

隐空间

隐空间表示给定数据分布的潜在表示，举个例子：

假设原始数据点 \(x \in ℝ^n\) ，是由一些低维向量 \(z \in ℝ^m\) 通过线性变换生成，具体而言：\(x=Az+v\)，其中 \(v\) 表示 n 维独立同分布的高斯噪声，并且 \(A \in ℝ^{n\times m}\) 。

通常，我们只能看到原始数据 \(x\)，无法知晓 \(z\)，这也是其为什么称为数据的潜在表示。然而我们希望得到 \(z\) ，因为它是数据更基础且压缩的表示。另外，潜在表示是很多算法很有用的输入。

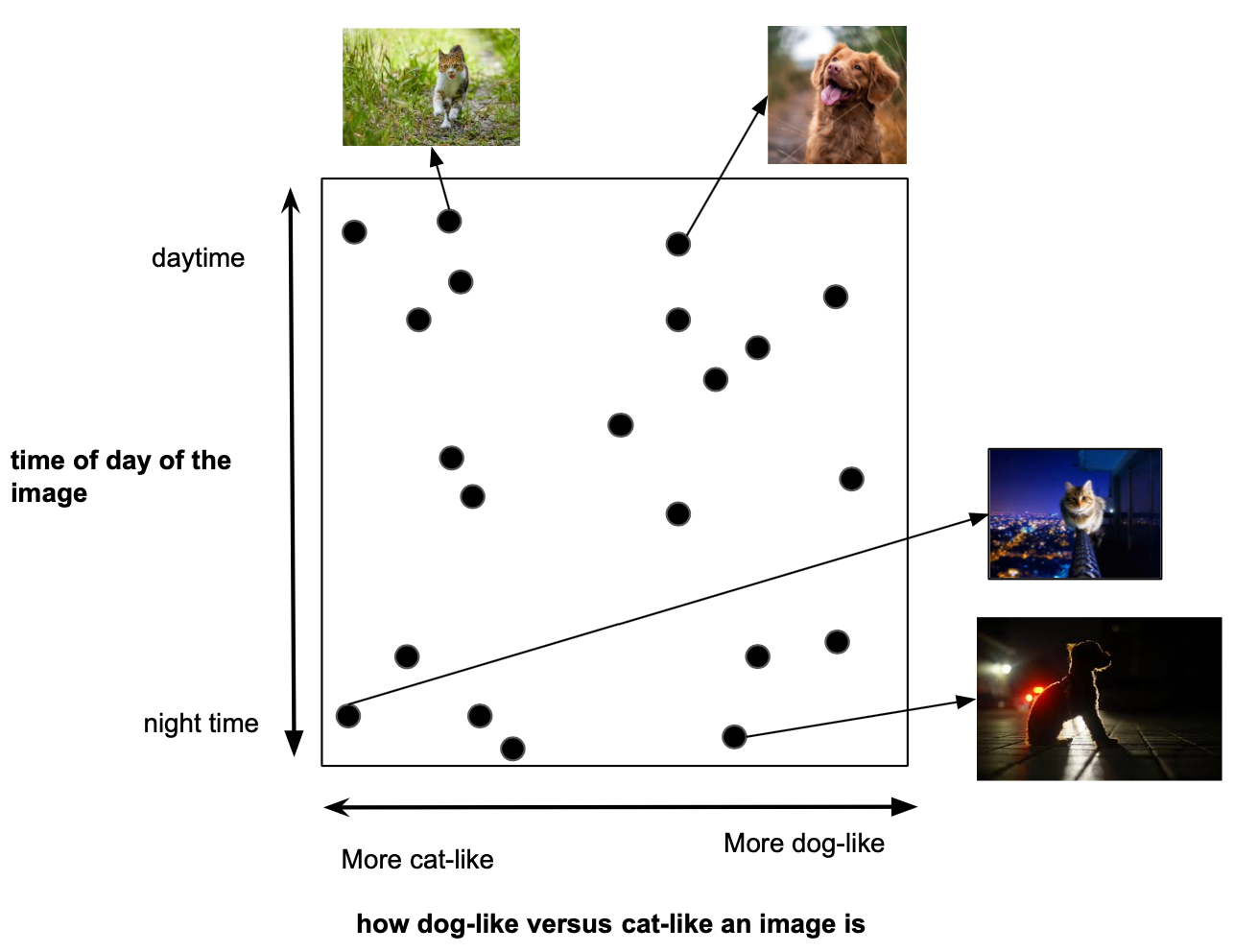
如果原始数据是隐变量的线性变换，正是经典无监督算法 PCA 的设计目的：PCA 本质上试图找到基础的 \(z\) 潜在表示。如果潜在表示与原始数据具有更复杂的非线性关系呢？例如，下图可视化了更复杂的隐空间可以编码的高级信息类型。在这种情况下，PCA 将无法找到最佳的潜在表示。我们可以使用自编码器来找到这个更抽象的隐空间。

注意：隐空间不需要是连续的向量空间，也可以是离散的，这也是 VQ-VAE 尝试寻找的隐空间类型。但在我们开始之前，让我们先了解一下原始的自编码器。

自编码器(AE)

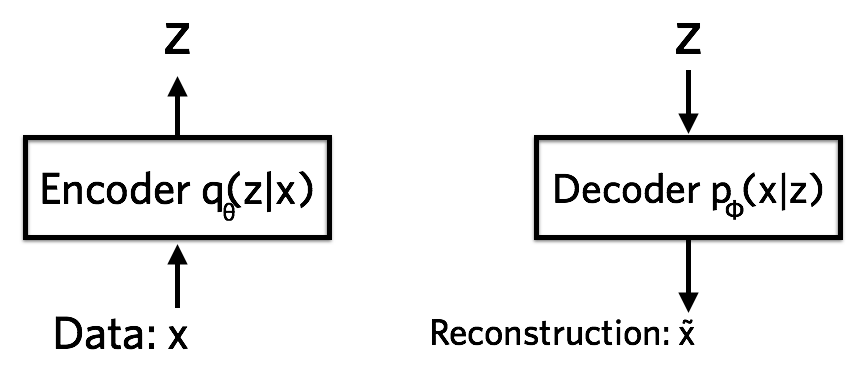
自编码器是一种无监督学习技术，它使用神经网络来寻找给定数据分布的非线性潜在表示。神经网络由两部分组成：编码网络(encoder) \(z=f(x)\) 和解码网路(decoder) \(\hat x=g(z)\) 。

这里 \(x\) 为输入数据，\(z\) 为隐变量表示，\(\hat x\) 表示从隐空间对 \(x\) 的重构，\(f(x)\) 和 \(g(z)\) 都是神经网络，将这两者组合在一起，整个模型可以表示为 \(\hat{x}=g(f(x))\) ，如下图：

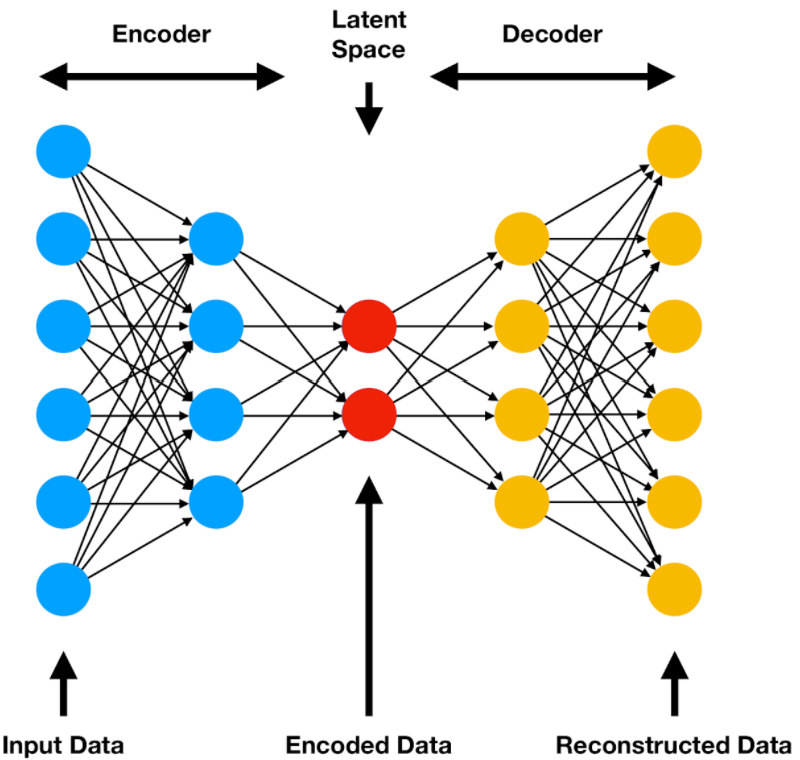
理想情况下，解码器应该能够准确地从编码器的潜在表示中重构原始数据。如果模型能够学习这样的重构，那么我们可以假设我们的隐空间能够很好地表示数据。为了实现这个目标，我们用某种 \(x\) 和 \(\hat x\) 的重构损失 \(\Vert x-\hat{x}\Vert_2^2\) 或 \(log(p(x\mid z))\) 来训练模型。

同样值得注意的是，\(z\) 的维数应始终低于 \(x\) 。毕竟，重点是对数据压缩编码，以便算法找到原始数据中最基本的部分。自编码器的这个压缩的、潜在部分通常也被称为网络的瓶颈，因为它将数据压缩到一个更小的空间里。

变分自编码器 (VAE)

（在这篇博客中不会详细介绍变分自编码器的所有数学细节，因为需要花一整篇博客来介绍 VAE。幸运的是，已经存在许多这样的博客，如果你想更详细地了解这个主题，推荐 Jaan Altosaar 的 这篇优秀的博客文章⁴。

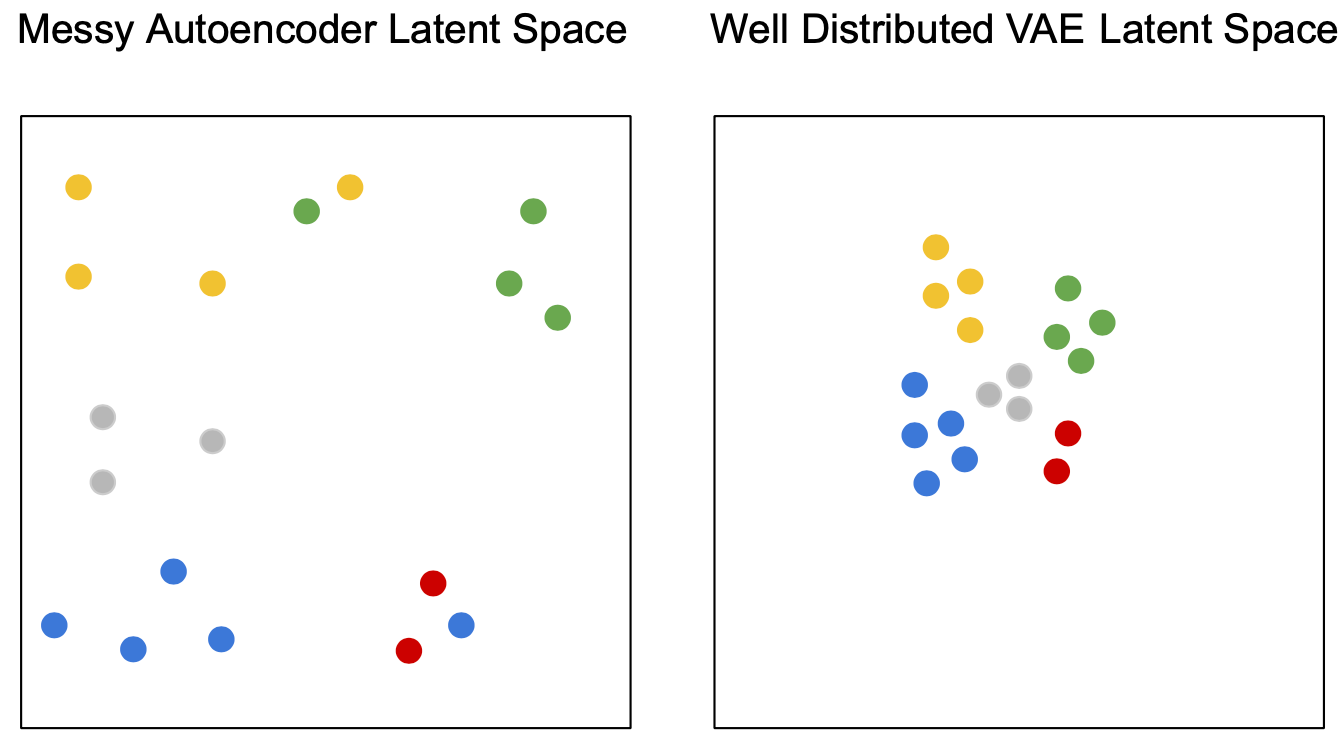
现在我们已经了解了自编码器的基本原理，让我们来看看变分自编码器的不同之处。关键区别在于 VAE 隐空间的结构。理想情况下，我们希望隐空间中语义相似的数据点彼此相邻，而语义不同的点彼此远离。最好的情况是，大部分数据分布在隐空间中构成紧凑的空间，而不是无限大。

原始的自编码器主要问题是，学习到的隐变量不一定具有这两种特性！该模型可以学习它想要的任何隐空间，它通常将数据点放在隐空间中很远的位置，并记住这些点。下图显示了自编码器隐空间的这些问题，并将其与 VAE 的进行了比较。

变分自编码器通过在隐空间上强制实施概率先验来克服这个问题。为了形式化这一点，将我们的潜在空间 \(z\) 视为随机变量。首先给隐变量一个先验 \(p(z)\) ，在多数的 VAEs 中，这只是一个高斯分布 \(\mathcal{N}(0, 1)\)，对于给定的原始数据点 \(x\)，我们也定义了一个隐空间的后验 \(p(z\mid x)\)。

我们最终目标是计算后验，可以用贝叶斯表示：

\[p(z|x)=\frac{p(x|z)p(z)}{p(x)}.\]

然而，我们处理的是连续变量，\(p(x)\) 难以计算。为了方便计算，我们将后验的近似限制在特定的分布族：独立高斯分布。称这个近似的分布为 \(q(z\mid x)\)。现在，我们的目标是最大限度地减少真正的后验和这种近似形式之间的 KL 差异。

这里将省略数学细节，但事实证明，可以通过最小化如下损失函数来计算此目标：

\[-E_{z \sim q(z|x)}[log(p(x|z))]+KL(q(z|x) || p(z))\]

上式中 \(q(z\mid x)\) 通过 encoder 近似，\(p(x\mid z)\) 由decoder 表示。

VAE 损失其实有一个很好的直观解释，第一项本质上是重构损失，第二项代表了后验的正则化。后验被 KL散度拉向先验，基本上将隐空间正则化为高斯先验，这可以让隐变量紧凑分布在 0 附近。

假设神经网络有足够表现力，VAE 隐空间可以非常好地拟合复杂数据分布。通常，您可以期望在隐空间中看到不同类型数据点的平滑过渡。例如，如果在 MNIST 上训练， 6 的集群和 5 的集群分隔开。在这两个聚类之间，可以得到一个看起来像 5 和 6 的奇怪混合数字。

总结

• 隐空间是数据的压缩表示，强调数据最重要的特征信息。
• 学习的隐变量对许多下游算法都很有用。
• 自编码器是一种用于寻找隐空间的方法，这些隐空间是数据的复杂非线性函数。
• 变分自编码器在自编码器基础上增加了一个先验隐空间，这为学习的隐空间提供了非常好的属性（我们可以通过隐空间平滑地插值数据分布）。

VQVAE

离散空间

我们已经掌握了自编码器的基础知识，现在就可以讨论 VQ-VAE 到底是什么。VAE 和 VQ-VAE 的根本区别在于 VAE 学习连续的潜在表示，而 VQ-VAE 学习离散的潜在表示。

到目前为止，我们已经看到了如何使用连续向量空间来表示自编码器中的隐变量。但隐变量不一定需要是连续向量，它实际上只需要是数据的一些数值表示。向量空间的一个潜在可替代方案是离散表示。

一般来说，我们在现实世界中遇到的许多数据都倾向于离散表示。例如，人类语音可以由离散的音素和语言很好地表示。此外，图像还包含具有一些离散限定符集的离散对象。可以想象用一个离散变量表示对象类型，一个用于表示其颜色，一个用于表示其大小，一个用于表示其方向，一个用于表示其形状，一个用于表示其纹理，一个用于表示背景颜色，一个用于表示背景纹理，等等……

除了表示之外，还有许多算法（如 transformers）旨在处理离散数据，因此我们希望有一个离散的数据表示供这些算法使用。

我们如何学习离散表示呢？乍一看，这似乎非常具有挑战性，因为一般来说，离散的东西在深度学习中并不太好做。幸运的是，VQ-VAE 设法使深度学习为这项任务工作，只需对原始自编码器做一些调整。

量化自编码器

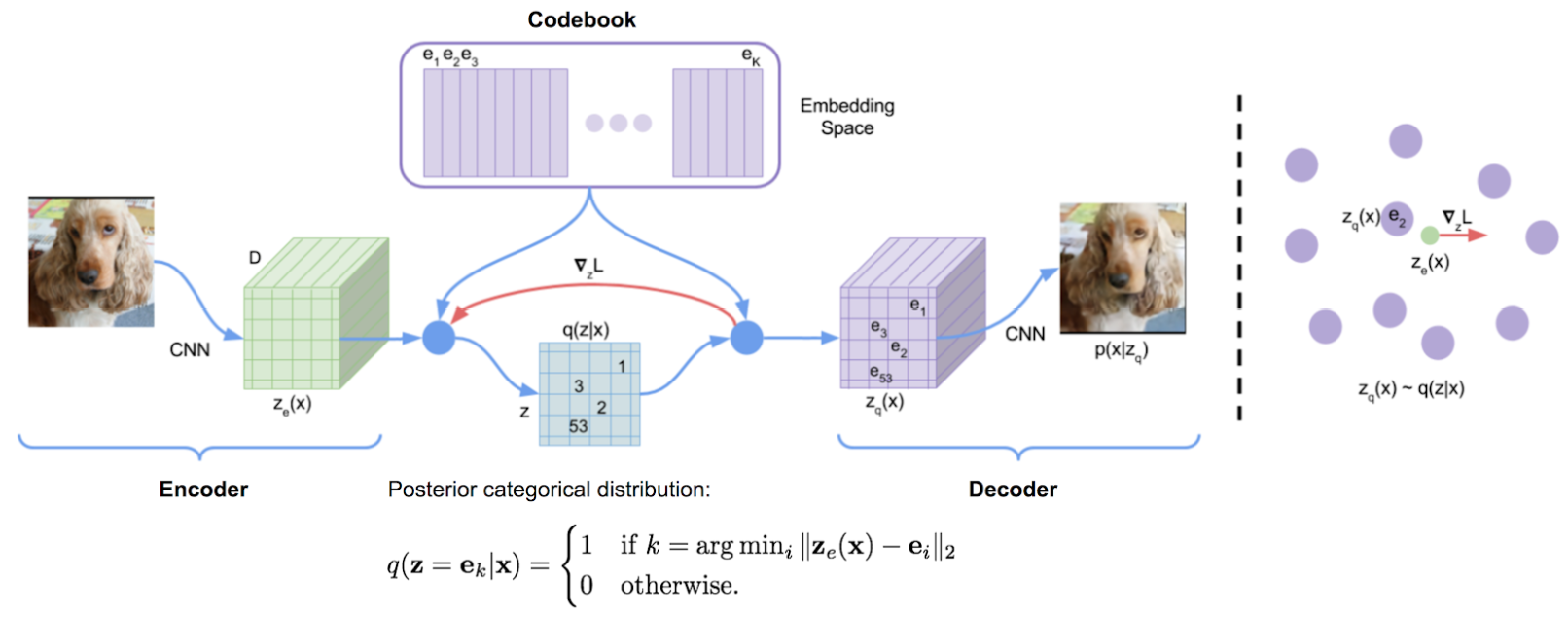
VQ-VAE 通过向网络添加离散的 codebook 组件来扩展标准自编码器。codebook 是与相应索引关联的向量列表。它用于量化自编码器的瓶颈；将编码器网络的输出与 codebook 的所有向量进行比较，并将欧氏距离最接近的 codebook 向量喂给解码器。

数学上可以写成 \(z_q(x)=\text{argmin}_i \Vert {z_e(x)-e_i }\Vert_2\) ，其中 \(z_e(x)\) 是原始输入的 encoder 向量，比如 \(i\) 表示第 \(i\) 个 codebook 向量，\(z_q(x)\) 表示生成的量化矢量，作为输入传递给解码器。

这个 \(\text{argmin}\) 操作有点令人担忧，因为它相对于编码器是不可微分的。但在实践中，可以通过这样的方式将 decoder 的梯度直接传递给 encoder （encoder 和 codebook 向量的梯度设置为1，其他 codebook 向量梯度设置为0）。

然后，解码器的任务是重构来自该量化矢量的输入，就像在标准自编码器公式中那样。

生成多个codes

您可能感到困惑的是，当解码器只能接受一组 codebook 向量作为输入时，人们怎么能指望它产生大量多样化的图像呢？

我们需要为每个训练点提供一个唯一的离散值，以便能够重建所有数据。如果情况确实如此，那么模型难道不会通过将每个训练点映射到不同的离散 code 来记住数据吗？

如果编码器只输出一个矢量，这的确会成为问题，但在实际的 VQ-VAE 中，编码器通常会产生一系列矢量。例如，对于图像，编码器可能会输出一个32x32 的矢量网格，每个网格都被量化，然后将整个网格送到解码器。所有向量都被量化为相同的 codebook，因此离散值的数量不会改变，但是通过输出多个codes，我们能够成倍地增加解码器可以构造的数据点的数量。

例如，假设我们正在处理图像，我们有一个尺寸为512的密码本，我们的编码器输出一个 32x32 的矢量网格。在这种情况下，我们的解码器可以输出 \(512^{32\times32}=2^{9216}\) 个不同图像！为了弄清楚这个数字有多大，我在下图中用python计算了它……这确实是一个深不可测的大数字。绝对没有人能够可视化这个模型的每个可能的输出。离散空间的大小在这里真的不再是问题。

当然，模型仍然可以记住训练数据，但是通过编码器中嵌入正确的归纳偏差（即对图像使用conv-net）和使用正确的隐变量结构（即用于图像的 32x32 网格），模型应该能够学习到一个很好地表示数据的离散空间。

学习 Codebook

就像编码器和解码器网络一样，codebook 通过梯度下降来学习的。理想情况下，我们的编码器将输出一个接近学习到的 codebook 向量。这里本质上存在一个双向问题：学习与编码器输出对齐的 codebook 向量和学习与codebook 向量对齐的编码器输出。

这两个问题可以通过向损失函数添加项来解决。整个VQ-VAE 损失函数是：

\[\text{log}(p(x|q(x)))+||\text{sg}[z_e(x)]-e||_2^2+\beta||z_e(x)-\text{sg}[e]||^2_2\]

在这里，我们使用与上一节中相同的符号，\(\text{sg}[x]\) 代表“停止梯度”。

第一项是标准的重构损失；第二项是 codebook 对齐损失，其目标是使所选的 codebook 矢量尽可能接近编码器输出。编码器输出有一个停止梯度运算符，因为这项仅用于更新 codebook。第三项与第二项类似，但它将停止梯度放在 codebook 向量上，因为它旨在更新编码器输出，让其尽可能接近 codebook 向量。这项称为codebook 损失，其对总体损失的重要性由超参数 \(\beta\) 调整。当然，如果有多个，则最后两项在模型的每个量化向量输出上取平均值。

这个损失函数基本上完成了我们对 VQ-VAE 的描述。

这样，我们可以完整地训练一个 VQ-VAE，能够重构一组不同的图像，这些图像与下图中的原始图像不同。我们还可以训练 VQ-VAE 来重构其他模态，如音频或视频。

从VAE角度解释VQ-VAE

现在我们已经了解了 VQ-VAE 的工作原理，让我们尝试在 VAE 提供的概率形式背景下理解它们。回想一下，VAE 在潜空间 \(p(z)\)上强制执行预定义的先验，编码器的任务是近似隐空间 \(p(z\mid x)\) 的后验分布。最后，解码器从隐空间 \(p(x\mid z)\) 重构。

在训练期间，VQ-VAE 假定所有隐变量具有统一的先验，因此所有隐变量都被视为具有同等的可能性。此外，后验是确定性的，因为如果 \(z=z_q(x)\) ,则 \(p(z\mid x)=1\)，否则为 0。最后，解码器分布 \(p(x\mid z)\) 保持不变，并像往常一样学习。

学习先验

一旦 VQ-VAE 训练完毕，我们就可以放弃在训练时的均匀先验，学习新的隐变量先验 \(p(z)\)。如果我们学习的先验可以准确表示离散 codes 的分布，我们将能够从该先验中采样并送到解码器生成新数据（原始 VQ-VAE 采样图像见下图）。

如果隐变量分布是不均匀的，那么表示隐变量序列的 bits 可以通过标准的霍夫曼或算术编码来对先验分布进一步压缩。

假设编码器可以为每个数据点输出一个隐变量序列，我们可以使用任何想要的自回归模型（ RNN 或 transformer）来训练先验。自回归因式分解，给定所有先前序列中的隐变量，预测下一个。这会将隐变量分布分解为 \(p(z)=p(z_1)p(z_2\mid z_1)p(z_3\mid z_1,z_2)p(z_4\mid z_1,z_2,z_3)...\)，其中 \(z_i\) 是序列中的第 \(i\) 个隐变量。

如果我们使用像音频这样的一维信号，那么将问题转换为自回归形式非常简单：只需从音频编码的 1-d 序列中预测下一个隐变量即可。对于图像，使用类似方法，首先将 32x32 的隐变量网格展开成一个 1-d 序列，使得序列从左上角到右下角，然后我们可以将自回归学习应用于此序列。

最新进展

这种训练 VQ-VAE 然后学习新的先验，正是 OpenAI 在其几个开创性的工作中使用的方法。OpenAI 的 jukebox⁵ 是一个能从原始音频中生成新音频的模型。 DALL-E涉及一个 transformer，该 transformer 以文本 embeddings 和在图像上训练的 VQ-VAE 的隐变量作为输入。

VQ-VAE 几乎比目前任何其他算法更好地表示多样化，复杂的数据分布。由于它与 transformers 配合得非常好，因此在给定足够大的计算预算的情况下，几乎可以扩展生成任意的可能性（不幸的是，对于最先进的结果，这是很少有个人甚至组织能够负担得起的预算）。出于这些原因，我预计 VQ-VAE 在相当长的一段时间内仍将是深度学习生态系统中的热门组件。

将在下一篇博客⁵中更仔细地研究 transformers 在单模态和多模态数据上进行自回归建模。

参考